
【题目】如图,在菱形![]() 中,
中,![]()
![]() 沿对角线
沿对角线![]() 将△
将△![]() 折起,使
折起,使![]() 之间的距离为
之间的距离为![]() 若
若![]() 分别为线段
分别为线段![]() 上的动点
上的动点

(1)求线段![]() 长度的最小值;
长度的最小值;
(2)当线段![]() 长度最小时,求直线
长度最小时,求直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】《乌鸦喝水》是《伊索寓言》中一个寓言故事。通过讲述一只乌鸦喝水的故事,告诉人们遇到困难要运用智慧、认真思考才能让问题迎刃而解的道理。如图2所示,乌鸦想喝水,发现有一个锥形瓶,上面部分是圆柱体,下面部分是圆台,瓶口直径为3厘米,瓶底直径为9厘米,瓶口距瓶颈为![]() 厘米,瓶颈到水位线距离和水位线到瓶底距离均为
厘米,瓶颈到水位线距离和水位线到瓶底距离均为![]() 厘米现将1颗石子投入瓶中,发现水位线上移
厘米现将1颗石子投入瓶中,发现水位线上移![]() 厘米,若只有当水位线到达瓶口时,乌鸦才能喝到水,则乌鸦共需要投入的石子数量至少是?(石子体积均视为一致)
厘米,若只有当水位线到达瓶口时,乌鸦才能喝到水,则乌鸦共需要投入的石子数量至少是?(石子体积均视为一致)
圆台体积公式:![]() ,其中,
,其中,![]() 为圆台高,
为圆台高,![]() 为圆台下底面半径,
为圆台下底面半径,![]() 为圆台上底面半径( )
为圆台上底面半径( )


A.2颗B.3颗C.4颗D.5颗
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】河图是上古时代神话传说中伏羲通过黄河中浮出龙马身上的图案,与自己的观察,画出的“八卦”,而龙马身上的图案就叫做“河图”.把一到十分成五组,如图,其口诀:一六共宗,为水居北;二七同道,为火居南;三八为朋,为木居东;四九为友,为金居西;五十同途,为土居中.“河图”将一到十分成五行属性分别为金,木,水,火,土的五组,在五行的五种属性中,五行相克的规律为:金克木,木克土,土克水,水克火,火克金;五行相生的规律为:木生火,火生土,土生金,金生水,水生木.现从这十个数中随机抽取3个数,则这3个数字的属性互不相克的条件下,取到属性为土的数字的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的两个顶点
的两个顶点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,且
,且![]() 所在直线的斜率之积等于
所在直线的斜率之积等于![]() ,记顶点
,记顶点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求顶点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 在曲线
在曲线![]() 上,且
上,且![]() 为
为![]() 的重心(
的重心(![]() 为坐标原点),求证:
为坐标原点),求证:![]() 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆C满足:圆心在
中,已知圆C满足:圆心在![]() 轴上,且与圆
轴上,且与圆![]() 相外切.设圆C与
相外切.设圆C与![]() 轴的交点为M,N,若圆心C在
轴的交点为M,N,若圆心C在![]() 轴上运动时,在
轴上运动时,在![]() 轴正半轴上总存在定点
轴正半轴上总存在定点![]() ,使得
,使得![]() 为定值,则点
为定值,则点![]() 的纵坐标为_________.
的纵坐标为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,
为等差数列,![]() 为等比数列,公比为
为等比数列,公比为![]() .令
.令![]() .
.
(1)若![]() .
.
①当![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
②设![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小?并证明你的结论.
的大小?并证明你的结论.
(2)问集合![]() 中最多有多少个元素?并证明你的结论.
中最多有多少个元素?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第18届国际篮联篮球世界杯(世界男子篮球锦标赛更名为篮球世界杯后的第二届世界杯)于2019年8月31日至9月15日在中国的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.中国队12名球员在第一场和第二场得分的茎叶图如图所示,则下列说法正确的是( )

A.第一场得分的中位数为![]() B.第二场得分的平均数为
B.第二场得分的平均数为![]()
C.第一场得分的极差大于第二场得分的极差D.第一场与第二场得分的众数相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 垂直平分线上的一点,且
垂直平分线上的一点,且![]() ,固定边
,固定边![]() ,在平面
,在平面![]() 内移动顶点
内移动顶点![]() ,使得
,使得![]() 的内切圆始终与
的内切圆始终与![]() 切于线段
切于线段![]() 的中点,且
的中点,且![]() 、
、![]() 在直线
在直线![]() 的同侧,在移动过程中,当
的同侧,在移动过程中,当![]() 取得最小值时,
取得最小值时,![]() 的面积为( )
的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程
的参数方程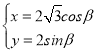 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程
的参数方程 (
(![]() 为参数).
为参数).
(1)求曲线![]() 在直角坐标系中的普通方程;
在直角坐标系中的普通方程;
(2)以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,当曲线
轴的正半轴为极轴建立极坐标系,当曲线![]() 截直线
截直线![]() 所得线段的中点极坐标为
所得线段的中点极坐标为![]() 时,求直线
时,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com