
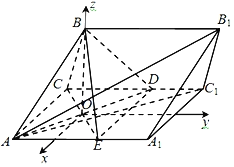
【题目】如图,在三棱柱ABC﹣A1B1C1中,已知四边形AA1C1C为矩形,AA1=6,AB=AC=4,∠BAC=∠BAA1=60°,∠A1AC的角平分线AD交CC1于D.
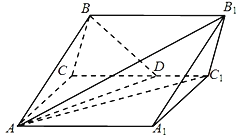
(1)求证:平面BAD⊥平面AA1C1C;
(2)求二面角A﹣B1C1﹣A1的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)过点D作DE∥AC交AA1于E,连接CE,BE,设AD∩CE=O,连接BO,推导出DE⊥AE,四边形AEDC为正方形,CE⊥AD,推导出△BAC≌△BAE,从而BC=BE,CE⊥BO,从而CE⊥平面BAD,由此能证明平面BAD⊥平面AA1C1C.
(2)推导出BO⊥AD,BO⊥CE,从而BO⊥平面AA1C1C,建立空间直角坐标系O﹣xyz,利用向量法能求出二面角A﹣B1C1﹣A1的余弦值.
解:(1)如图,过点D作DE∥AC交AA1于E,连接CE,BE,
设AD∩CE=O,连接BO,∵AC⊥AA1,∴DE⊥AE,
又AD为∠A1AC的角平分线,∴四边形AEDC为正方形,∴CE⊥AD,
又∵AC=AE,∠BAC=∠BAE,BA=BA,∴![]() BAC≌
BAC≌![]() BAE,∴BC=BE,
BAE,∴BC=BE,
又∵O为CE的中点,∴CE⊥BO,
又∵AD,BO![]() 平面BAD,AD∩BO=O,∴CE⊥平面BAD.
平面BAD,AD∩BO=O,∴CE⊥平面BAD.
又∵CE![]() 平面AA1C1C,∴平面BAD⊥平面AA1C1C.
平面AA1C1C,∴平面BAD⊥平面AA1C1C.
(2)在![]() ABC中,∵AB=AC=4,∠BAC=60°,∴BC=4,
ABC中,∵AB=AC=4,∠BAC=60°,∴BC=4,
在Rt![]() BOC中,∵
BOC中,∵![]() ,∴
,∴![]() ,
,
又AB=4,![]() ,∵BO2+AO2=AB2,∴BO⊥AD,
,∵BO2+AO2=AB2,∴BO⊥AD,
又BO⊥CE,AD∩CE=O,AD,CE![]() 平面AA1C1C,∴BO⊥平面AA1C1C,
平面AA1C1C,∴BO⊥平面AA1C1C,
故建立如图空间直角坐标系O﹣xyz,
则A(2,﹣2,0),A1(2,4,0),C1(﹣2,4,0),![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
设平面AB1C1的一个法向量为![]() ,
,
则 ,∴
,∴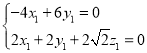 ,
,
令x1=6,得![]() ,
,
设平面A1B1C1的一个法向量为![]() ,
,
则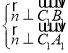 ,∴
,∴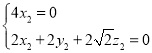 ,
,
令![]() ,得
,得![]() ,
,
∴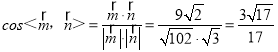 ,
,
故二面角A﹣B1C1﹣A1的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年3月10日湖北武汉某方舱医院“关门大吉”,某省驰援湖北“抗疫”的9名身高各不相同的医护人员站成一排合影留念,庆祝圆满完成“抗疫”任务,若恰好从中间往两边看都依次变低,则身高排第4的医护人员和最高的医护人员相邻的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上运动,
轴上运动,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 方程;
方程;
(2)动直线![]() 与
与![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,且
,且![]() 的面积为
的面积为![]() ,其中
,其中![]() 为坐标原点,证明
为坐标原点,证明![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等比数列,其前
为等比数列,其前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() .
.![]() 为等差数列,其前
为等差数列,其前![]() 项和为
项和为![]() ,如图_____,
,如图_____,![]() 的图象经过
的图象经过![]() 两个点.
两个点.
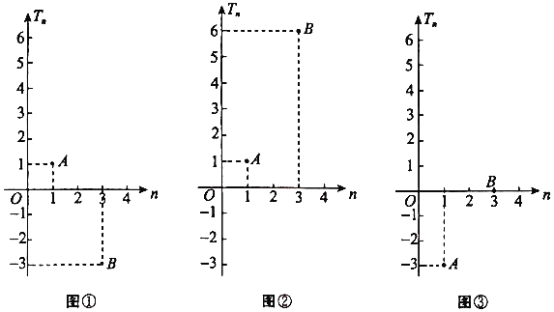
(Ⅰ)求![]() ;
;
(Ⅱ)若存在正整数![]() ,使得
,使得![]() ,求
,求![]() 的最小值.从图①,图②,图③中选择一个适当的条件,补充在上面问题中并作答.
的最小值.从图①,图②,图③中选择一个适当的条件,补充在上面问题中并作答.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2019年9月到2020年2月这半年中,某个关键词的搜索指数变化的走势图.
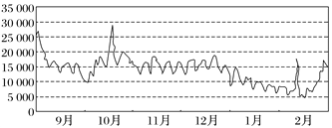
根据该走势图,下列结论不正确的是( ).
A.这半年中,网民对该关键词相关的信息关注度与时间具有比较明显的线性相关性
B.2019年10月网民对该关键词的搜索指数变化的走势图具有较好的对称性,与正态曲线相近,故当月搜索指数的平均值约为29000
C.从网民对该关键词的搜索指数来看,2019年10月的方差小于11月的方差
D.从网民对该关键词的搜索指数来看,2019年12月的平均值大于2020年1月的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体![]() 中,
中,![]() 是棱
是棱![]() 的中点,
的中点,![]() 是侧面
是侧面![]() 上的动点,且
上的动点,且![]() 平面
平面![]() ,记
,记![]() 与
与![]() 的轨迹构成的平面为
的轨迹构成的平面为![]() .
.
①![]() ,使得
,使得![]() ;
;
②直线![]() 与直线
与直线![]() 所成角的正切值的取值范围是
所成角的正切值的取值范围是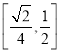 ;
;
③![]() 与平面
与平面![]() 所成锐二面角的正切值为
所成锐二面角的正切值为![]() ;
;
④正方体![]() 的各个侧面中,与
的各个侧面中,与![]() 所成的锐二面角相等的侧面共四个.
所成的锐二面角相等的侧面共四个.
其中正确命题的序号是________.(写出所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com