
【题目】如图,已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形, 且∠DAB=90°,∠ABC=45°,CB= ![]() ,AB=2,PA=1
,AB=2,PA=1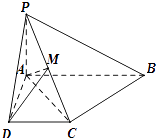
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
(3)若M是PC的中点,求三棱锥C﹣MAD的体积.
【答案】
(1)∵底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,
∴AB∥CD,
又AB平面PCD,CD平面PCD,
∴AB∥平面PCD
(2)∵∠ABC=45°,CB= ![]() ,AB=2,
,AB=2,
∴AC2=AB2+BC2﹣2ABBCcos45°= ![]() =2.
=2.
则AC2+BC2=AB2,∴BC⊥AC.
∵PA⊥平面ABCD,BC平面ABCD,∴PA⊥BC.
又PA∩AC=A,∴BC⊥平面PAC
(3)在直角梯形ABCD中,过C作CE⊥AB于点E,
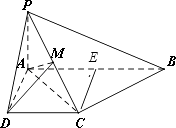
则四边形ADCE为矩形,∴AE=DC,AD=EC.
在Rt△CEB中,可得BE=BCcos45°= ![]() ,
,
CE=BCsin45°= ![]() ,∴AE=AB﹣BE=2﹣1=1
,∴AE=AB﹣BE=2﹣1=1
∴S△ADC= ![]() =
= ![]() =
= ![]() .,
.,
∵M是PC的中点,∴M到平面ADC的距离是P到平面ADC距离的一半,
∴VC﹣MAD=VM﹣ACD= ![]() ×S△ACD×(
×S△ACD×( ![]() PA)=
PA)= ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
【解析】(1)利用线面平行的判定定理证明;(2)利用勾股定理证明BC⊥AC,由PA⊥平面ABCD,可得PA⊥BC.从而可证得BC⊥平面PAC:(3)在直角梯形ABCD中,过C作CE⊥AB于点E,则四边形ADCE为矩形,AE=DC,AD=EC.求得CE,计算△ACD的面积,根据M到平面ADC的距离是P到平面ADC距离的一半,求得棱锥的高,代入体积公式计算.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,侧面
的正方形,侧面![]()
底面![]() ,且
,且![]() ,
, ![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:面![]() 平面
平面![]() ;
;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 和抛物线
和抛物线![]() :
: ![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)已知直线![]() 和圆
和圆![]() 相切,与抛物线
相切,与抛物线![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)过抛物线![]() 上一点
上一点![]() 作两直线
作两直线![]() 和圆
和圆![]() 相切,且分别交抛物线
相切,且分别交抛物线![]() 于
于![]() 两点,若直线
两点,若直线![]() 的斜率为
的斜率为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】六个面都是平行四边形的四棱柱称为平行六面体.已知在平行四边形ABCD中(如图1),有AC2+BD2=2(AB2+AD2),则在平行六面体ABCD﹣A1B1C1D1中(如图2),AC12+BD12+CA12+DB12等于( ) 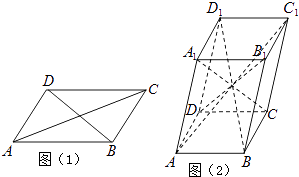
A.2(AB2+AD2+AA12)
B.3(AB2+AD2+AA12)
C.4(AB2+AD2+AA12)
D.4(AB2+AD2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题: 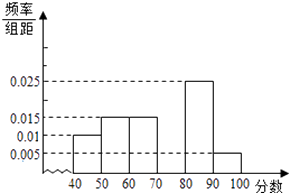
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P(x,y)满足方程xy=1(x>0).
(Ⅰ)求动点P到直线l:x+2y﹣ ![]() =0距离的最小值;
=0距离的最小值;
(Ⅱ)设定点A(a,a),若点P,A之间的最短距离为2 ![]() ,求满足条件的实数a的取值.
,求满足条件的实数a的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点. 
(1)求证:平面DFG∥平面ABE;
(2)若AC=2BC=2CD=4,求二面角E﹣AB﹣C的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个单位有职工800人,期中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是( )
A.12,24,15,9
B.9,12,12,7
C.8,15,12,5
D.8,16,10,6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com