
【题目】已知动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两个不同点,且
两个不同点,且![]() 的面积
的面积![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)证明![]() 和
和![]() 均为定值;
均为定值;
(2)设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的最大值;
的最大值;
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)对直线![]() 的斜率是否存在进行分类讨论,在直线
的斜率是否存在进行分类讨论,在直线![]() 的斜率不存在时,可得出
的斜率不存在时,可得出![]() ,
,![]() ,根据
,根据![]() 的面积求得
的面积求得![]() 、
、![]() 的值,可得出
的值,可得出![]() 和
和![]() 的值;在直线
的值;在直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 的方程与椭圆的方程联立,列出韦达定理,利用三角形的面积公式可求得
的方程与椭圆的方程联立,列出韦达定理,利用三角形的面积公式可求得![]() 和
和![]() 的值,进而得出结论;
的值,进而得出结论;
(2)对直线![]() 的斜率是否存在进行分类讨论,在直线
的斜率是否存在进行分类讨论,在直线![]() 的斜率不存在时,可直接求得
的斜率不存在时,可直接求得![]() 的值;在直线
的值;在直线![]() 的斜率存在时,求得
的斜率存在时,求得![]() 、
、![]() 关于
关于![]() 的表达式,利用基本不等式可求得
的表达式,利用基本不等式可求得![]() 的最大值,进而可得出结论.
的最大值,进而可得出结论.
(1)当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 、
、![]() 两点关于
两点关于![]() 轴对称,所以
轴对称,所以![]() ,
,![]() ,
,
![]() 在椭圆上,
在椭圆上,![]() ①,又
①,又![]() ,②
,②
由①②得![]() ,
,![]() .此时
.此时![]() ,
,![]() ;
;
当直线![]() 的斜率存在时,是直线
的斜率存在时,是直线![]() 的方程为
的方程为![]() ,
,
将直线![]() 的方程代入
的方程代入![]() 得
得![]() ,
,
![]() ,即
,即![]() ,
,
由韦达定理得![]() ,
,![]() ,
,
![]() ,
,
![]() 点O到直线
点O到直线![]() 的距离为
的距离为![]() ,
,
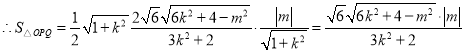 ,
,
又![]() ,整理得
,整理得![]() ,
,
此时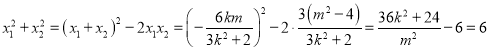 ,
,
![]() ,
,
综上所述![]() ,
,![]() ,结论成立;
,结论成立;
(2)当直线![]() 的斜率不存在时,由(1)知
的斜率不存在时,由(1)知![]() ,
,![]() ,因此
,因此![]() ;
;
当直线![]() 的斜率存在时,由(1)知
的斜率存在时,由(1)知![]() ,
,![]() ,
,
![]() ,
,
 ,
,
所以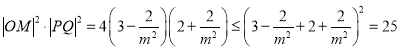 ,
,![]() .
.
当且仅当![]() ,即
,即![]() 时,等号成立.
时,等号成立.
综上所述,![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,P是上底面A1B1C1D1内一点,若AP∥平面BDEF,则线段AP长度的取值范围是( )
A.[![]() ,
,![]() ]B.[
]B.[![]() ,
,![]() ]C.[
]C.[![]() ,
,![]() ]D.[
]D.[![]() ,
,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
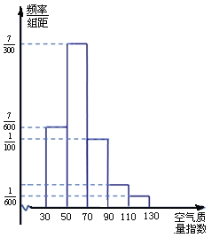
【题目】某市积极贯彻落实国务院《“十三五”节能减排综合工作方案》,空气质量明显改善.该市生态环境局统计了某月(30天)空气质量指数,绘制成如下频率分布直方图.已知空气质量等级与空气质量指数对照如下表:
空气质量指数 |
|
|
|
|
| 300以上 |
空气质量等级 | 一级 (优) | 二级 (良) | 三级 (轻度污染) | 四级 (中度污染) | 五级 (重度污染) | 六级 (严重污染) |
(1)根据频率分布直方图估计,在这30天中,空气质量等级为优或良的天数;
(2)根据体质检查情况,医生建议:当空气质量指数高于90时,市民甲不宜进行户外体育运动;当空气质量指数高于70时,市民乙不宜进行户外体育运动(两人是否进行户外体育运动互不影响).
①从这30天中随机选取2天,记乙不宜进行户外体育运动,且甲适宜进行户外体育运动的天数为X,求X的分布列和数学期望;
②以该月空气质量指数分布的频率作为以后每天空气质量指数分布的概率(假定每天空气质量指数互不影响),甲、乙两人后面分别随机选择3天和2天进行户外体育运动,求甲恰有2天,且乙恰有1天不宜进行户外体育运动的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsinθ=2.
(1)M为曲线C1上的动点,点P在线段OM上,且满足![]() ,求点P的轨迹C2的直角坐标方程;
,求点P的轨迹C2的直角坐标方程;
(2)曲线C2上两点![]() 与点B(ρ2,α),求△OAB面积的最大值.
与点B(ρ2,α),求△OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立直角坐标系,过点
轴建立直角坐标系,过点![]() 作倾斜角为
作倾斜角为![]() (
(![]() )的直线
)的直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的直角坐标方程,并写出直线
的直角坐标方程,并写出直线![]() 的参数方程;
的参数方程;
(2)过点![]() 的另一条直线
的另一条直线![]() 与
与![]() 垂直,且与曲线
垂直,且与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】辊子是客家传统农具,南方农民犁开田地后,仍有大的土块.农人便用六片叶齿组成辊轴,两侧装上木板,人跨开两脚站立,既能掌握平衡,又能增加重量,让牛拉动辊轴前进,压碎土块,以利于耕种.这六片叶齿又对应着菩萨六度,即布施持戒忍辱精进禅定与般若.若甲乙每人依次有放回地从这六片叶齿中随机取一片,则这两人选的叶齿对应的“度”相同的概率为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com