
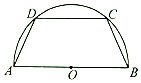
 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠DAB=θ(0<θ<$\frac{π}{2}$),L为等腰梯形ABCD的周长.
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠DAB=θ(0<θ<$\frac{π}{2}$),L为等腰梯形ABCD的周长.分析 (1)由于AB是圆O的直径,所以三角形ABD是直角三角形,连BD,过D作DE⊥AB于E,则由射影定理可知AD2=AE•AB,从而可用腰长表示上底长,进而可求梯形的周长y与腰长x之间的函数关系式,根据上底长,可确定函数的定义域;
(2)令t=cosθ,由$0<θ<\frac{π}{2}$,知t∈(0,1).利用配方法可知函数函数在(0,$\frac{1}{2}$)上单调递增,在($\frac{1}{2}$,1)单调递减,由此可求周长y的最大值.
解答 解:(1)连接BD,则∠ADB=90°,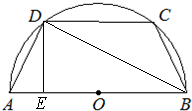
∴AD=BC=4cosθ.…(2分)
作DE⊥AB于M,CN⊥AB于N,
得AM=BN=ADcosθ=4cos2θ,
∴DC=AB-2AM=4-8cos2θ. …(4分)
∴△ABC的周长L=AB+2AD+DC=4+8cosθ+(4-8cos2θ)=8+8cosθ-8cos2θ. …(5分)
(2)令t=cosθ,由$0<θ<\frac{π}{2}$,知t∈(0,1).
则$L=-8{t^2}+8t+8=-8{(t-\frac{1}{2})^2}+10$,…(8分)
当t=$\frac{1}{2}$,即$cosθ=\frac{1}{2}$,$θ=\frac{π}{3}$时,L有最大值10.
∴当θ=60°时,L存在最大值10.…(10分)
点评 本题以半圆为载体,考查函数模型的构建,关键是腰长表示上底长,同时考查二次函数的最值求法.


科目:高中数学 来源: 题型:选择题
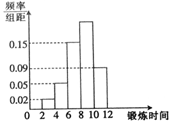 某校有150位教职员工,其每周用于锻炼身体所用时间的频率分布直方图如图所示,据图估计,锻炼时间在[8,10)小时内的人数为( )
某校有150位教职员工,其每周用于锻炼身体所用时间的频率分布直方图如图所示,据图估计,锻炼时间在[8,10)小时内的人数为( )| A. | 30 | B. | 120 | C. | 57 | D. | 93 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$ | B. | 16 | C. | $\frac{1}{4}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | $2\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com