
已知函数f(x)=x3+x-16.
(1)求曲线y=f(x)在点(2,-6)处的切线方程.
(2)如果曲线y=f(x)的某一切线与直线y=- x+3垂直,求切点坐标与切线的方程.
x+3垂直,求切点坐标与切线的方程.
(1) y=13x-32 (2) 切点坐标为(1,-14)或(-1,-18) y=4x-18或y=4x-14
【解析】(1)可判定点(2,-6)在曲线y=f(x)上.
∵f'(x)=(x3+x-16)'=3x2+1,
∴在点(2,-6)处的切线的斜率为k=f'(2)=13,
∴切线的方程为y=13(x-2)+(-6),
即y=13x-32.
(2)∵切线与直线y=-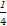 x+3垂直,
x+3垂直,
∴切线的斜率k=4.
设切点的坐标为(x0,y0),则f'(x0)=3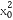 +1=4,
+1=4,
∴x0=±1,
∴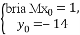 或
或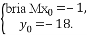
∴切点坐标为(1,-14)或(-1,-18),
切线方程为y=4(x-1)-14或y=4(x+1)-18.
即y=4x-18或y=4x-14.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十二第二章第九节练习卷(解析版) 题型:选择题
某学校制定奖励条例,对在教育教学中取得优异成绩的教职工实行奖励,其中有一个奖励项目是针对学生高考成绩的高低对任课教师进行奖励的.奖励公式为f(n)=k(n)(n-10),n>10(其中n是任课教师所在班级学生的该任课教师所教学科的平均成绩与该科省平均分之差,f(n)的单位为元),而k(n)=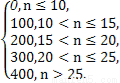 现有甲、乙两位数学任课教师,甲所教的学生高考数学平均分超出省平均分18分,而乙所教的学生高考数学平均分超出省平均分21分,则乙所得奖励比甲所得奖励多( )
现有甲、乙两位数学任课教师,甲所教的学生高考数学平均分超出省平均分18分,而乙所教的学生高考数学平均分超出省平均分21分,则乙所得奖励比甲所得奖励多( )
(A)600元 (B)900元 (C)1600元 (D)1700元
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:选择题
函数y=4sin(2x+ )的一个单调区间是 ( )
)的一个单调区间是 ( )
(A)[ ,
,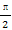 ] (B)[-
] (B)[-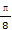 ,
,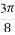 ]
]
(C)[0,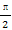 ] (D)[0,
] (D)[0,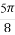 ]
]
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:选择题
已知函数f(x)=sin(2x-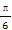 ),若存在a∈(0,π),使得f(x+a)=f(x-a)恒成立,则a的值是( )
),若存在a∈(0,π),使得f(x+a)=f(x-a)恒成立,则a的值是( )
(A)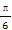 (B)
(B)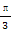 (C)
(C) (D)
(D)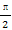
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十一第二章第八节练习卷(解析版) 题型:解答题
已知二次函数f(x)=x2+(2a-1)x+1-2a.
(1)判断命题“对于任意的a∈R(R为实数集),方程f(x)=1必有实数根”的真假,并写出判断过程.
(2)若y=f(x)在区间(-1,0)及(0, )内各有一个零点,求实数a的范围.
)内各有一个零点,求实数a的范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十六第十章第三节练习卷(解析版) 题型:解答题
已知(1+x+mx2)10的展开式中x4的系数大于-330,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com