
【题目】已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b﹣2c)cosA=a﹣2acos2 ![]() .
.
(1)求角A的值;
(2)若a= ![]() ,则求b+c的取值范围.
,则求b+c的取值范围.
【答案】
(1)解:在锐角△ABC中,根据(b﹣2c)cosA=a﹣2acos2 ![]() =a﹣2a
=a﹣2a ![]() ,
,
利用正弦定理可得 (sinB﹣2sinC)cosA=sinA(﹣cosB),
即 sinBcosA+cosBsinA=2sinCcosA,即sin(B+A)=2sinCcosA,
即sinC=2sinCcosA,∴cosA= ![]() ,∴A=
,∴A= ![]()
(2)解:若a= ![]() ,则由正弦定理可得
,则由正弦定理可得 ![]() =
= ![]() =2,
=2,
∴b+c=2(sinB+sinC)=2[sinB+sin( ![]() ﹣B)]=3sinB+
﹣B)]=3sinB+ ![]() cosB=2
cosB=2 ![]() sin(B+
sin(B+ ![]() ).
).
由于 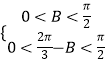 ,求得
,求得 ![]() <B<
<B< ![]() ,∴
,∴ ![]() <B+
<B+ ![]() <
< ![]() .
.
∴sin(B+ ![]() )∈(
)∈( ![]() ,1],∴b+c∈(3,2
,1],∴b+c∈(3,2 ![]() ]
]
【解析】(1)在锐角△ABC中,根据条件利用正弦定理可得 (sinB﹣2sinC)cosA=sinA(﹣cosB),化简可得cosA = ![]() ,由此可得A的值.(2)由正弦定理可得
,由此可得A的值.(2)由正弦定理可得 ![]() =
= ![]() =2,可得 b+c=2(sinB+sinC)=2
=2,可得 b+c=2(sinB+sinC)=2 ![]() sin(B+
sin(B+ ![]() ).
).
再由  ,求得B的范围,再利用正弦函数的定义域和值域求得b+c的取值范围.
,求得B的范围,再利用正弦函数的定义域和值域求得b+c的取值范围.


科目:高中数学 来源: 题型:
【题目】已知数列 ![]() 的前
的前 ![]() 项和为
项和为 ![]() ,且满足
,且满足 ![]() ,求数列
,求数列 ![]() 的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
思路1:先设 ![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出 ![]() ,
, ![]() ,
, ![]() .
.
猜想: ![]() .
.
然后用数学归纳法证明.证明过程如下:
①当 ![]() 时, , 猜想成立
时, , 猜想成立
②假设 ![]() (
( ![]() N*)时,猜想成立,即
N*)时,猜想成立,即 ![]() .
.
那么,当 ![]() 时,由已知
时,由已知 ![]() ,得
,得 ![]() .
.
又 ![]() ,两式相减并化简,得
,两式相减并化简,得 ![]() (用含
(用含 ![]() 的代数式表示).
的代数式表示).
所以,当 ![]() 时,猜想也成立.
时,猜想也成立.
根据①和②,可知猜想对任何 ![]() N*都成立.
N*都成立.
思路2:先设 ![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出 ![]() .
.
由已知 ![]() ,写出
,写出 ![]() 与
与 ![]() 的关系式:
的关系式: ![]() ,
,
两式相减,得 ![]() 与
与 ![]() 的递推关系式:
的递推关系式: ![]() .
.
整理: ![]() .
.
发现:数列 ![]() 是首项为 , 公比为的等比数列.
是首项为 , 公比为的等比数列.
得出:数列 ![]() 的通项公式
的通项公式 ![]() , 进而得到
, 进而得到 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:x∈(﹣∞,0),2x>3x;命题q:x∈(0,+∞), ![]() >x3; 则下列命题中真命题是( )
>x3; 则下列命题中真命题是( )
A.p∧q
B.(¬p)∧q
C.(¬p)∨(¬q)
D.p∧(¬q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四棱锥 ![]() 中,四边形
中,四边形 ![]() 为平行四边形,
为平行四边形, ![]() 为等边三角形,AABE是以
为等边三角形,AABE是以 ![]() 为直角的等腰直角三角形,且
为直角的等腰直角三角形,且 ![]() .
.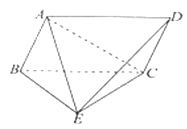
(1)证明: 平面 ![]() 平面BCE;
平面BCE;
(2)求二面角 ![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(x+φ)(A>0,0<<4,|φ|< ![]() )过点(0,
)过点(0, ![]() ),且当x=
),且当x= ![]() 时,函数f(x)取得最大值1.
时,函数f(x)取得最大值1.
(1)将函数f(x)的图象向右平移 ![]() 个单位得到函数g(x),求函数g(x)的表达式;
个单位得到函数g(x),求函数g(x)的表达式;
(2)在(1)的条件下,函数h(x)=f(x)+g(x)+2cos2x﹣1,如果对于x1 , x2∈R,都有h(x1)≤h(x)≤h(x2),求|x1﹣x2|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴、y轴上的截距相等,求切线的方程;
(2)从圆C外一点P(x1 , y1)向圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使|PM|最小的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=asinx﹣bcosx(a,b为常数,a≠0,x∈R)在x= ![]() 处取得最小值,则函数g(x)=f(
处取得最小值,则函数g(x)=f( ![]() ﹣x)是( )
﹣x)是( )
A.偶函数且它的图象关于点 (π,0)对称
B.奇函数且它的图象关于点 (π,0)对称
C.奇函数且它的图象关于点( ![]() . ,0)对称
. ,0)对称
D.偶函数且它的图象关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min,山路AC长为1260 m,经测量,cos A=![]() ,cos C=
,cos C=![]()
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,SB⊥底面ABC,且SB=AB=2,BC= ![]() ,D、E分别是SA、SC的中点.
,D、E分别是SA、SC的中点.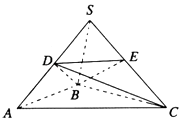
(I)求证:平面ACD⊥平面BCD;
(II)求二面角S﹣BD﹣E的平面角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com