
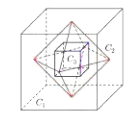
【题目】如图,记棱长为1的正方体![]() ,以
,以![]() 各个面的中心为顶点的正八面体为
各个面的中心为顶点的正八面体为![]() ,以
,以![]() 各面的中心为顶点的正方体为
各面的中心为顶点的正方体为![]() ,以
,以![]() 各个面的中心为顶点的正八面体为
各个面的中心为顶点的正八面体为![]() ,……,以此类推得一系列的多面体
,……,以此类推得一系列的多面体![]() ,设
,设![]() 的棱长为
的棱长为![]() ,则数列
,则数列![]() 的各项和为________.
的各项和为________.
科目:高中数学 来源: 题型:
【题目】已知焦点在x轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点![]() 为圆心,1为半径的圆相切,又知C的一个焦点与P关于直线
为圆心,1为半径的圆相切,又知C的一个焦点与P关于直线![]() 对称.
对称.
(1)求双曲线C的方程;
(2)设直线![]() 与双曲线C的左支交于A、B两点,另一直线
与双曲线C的左支交于A、B两点,另一直线![]() 经过
经过![]() 及AB的中点,求直线
及AB的中点,求直线![]() 在y轴上的截距b的取值范围;
在y轴上的截距b的取值范围;
(3)若Q是双曲线C上的任一点,![]() 、
、![]() 为双曲线C的左、右两个焦点,从
为双曲线C的左、右两个焦点,从![]() 引
引![]() 的角平分线的垂线,垂足为N,试求点N的轨迹方程.
的角平分线的垂线,垂足为N,试求点N的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校y(百个) | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱.
(已知:![]() ,则认为y与x线性相关性很强;
,则认为y与x线性相关性很强;![]() ,则认为y与x线性相关性一般;
,则认为y与x线性相关性一般;![]() ,则认为y与x线性相关性较):
,则认为y与x线性相关性较):
(2)求y关于x的线性回归方程,并预测A地区2020年足球特色学校的个数(精确到个).
参考公式和数据: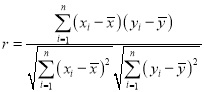 ,
,
![]()
![]()
![]() ,
,
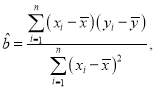
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(理)已知数列![]() 满足
满足![]() (
(![]() ),首项
),首项![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)数列![]() 满足
满足![]() ,记数列
,记数列 的前
的前![]() 项和为
项和为![]() ,
,![]() 是△ABC的内角,若
是△ABC的内角,若![]() 对于任意
对于任意![]() 恒成立,求角
恒成立,求角![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班学生中喜爱看综艺节目的有18人,体育节目的有27人,时政节目的有9人,现采取分层抽样的方法从这些学生中抽取6名学生.
(Ⅰ)求应从喜爱看综艺节目,体育节目,时政节目的学生中抽取的学生人数;
(Ⅱ)若从抽取的6名学生中随机抽取2人分作一组,
(1)列出所有可能的结果;
(2)求抽取的2人中有1人喜爱综艺节目1人喜爱体育节目的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业参加![]() 项目生产的工人为
项目生产的工人为![]() 人,平均每人每年创造利润
人,平均每人每年创造利润![]() 万元.根据现实的需要,从
万元.根据现实的需要,从![]() 项目中调出
项目中调出![]() 人参与
人参与![]() 项目的售后服务工作,每人每年可以创造利润
项目的售后服务工作,每人每年可以创造利润![]() 万元(
万元(![]() ),
),![]() 项目余下的工人每人每年创造利图需要提高
项目余下的工人每人每年创造利图需要提高![]()
(1)若要保证![]() 项目余下的工人创造的年总利润不低于原来
项目余下的工人创造的年总利润不低于原来![]() 名工人创造的年总利润,则最多调出多少人参加
名工人创造的年总利润,则最多调出多少人参加![]() 项目从事售后服务工作?
项目从事售后服务工作?
(2)在(1)的条件下,当从![]() 项目调出的人数不能超过总人数的
项目调出的人数不能超过总人数的![]() 时,才能使得
时,才能使得![]() 项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数
项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产的某批产品的销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为正常数).已知生产该产品还需投入成本
为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为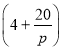 元
元![]() 件.
件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,该公司的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图是某校高三(1)班的一次数学知识竞赛成绩的茎叶图(图中仅列出![]() ,
,![]() 的数据)和频率分布直方图.
的数据)和频率分布直方图.
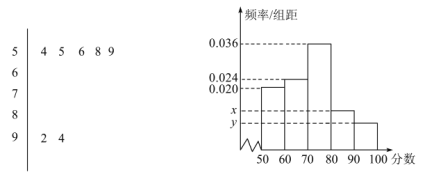
(1)求分数在![]() 的频率及全班人数;
的频率及全班人数;
(2)求频率分布直方图中的![]() ;
;
(3)若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com