
 =(-a,a,a),
=(-a,a,a), =(0,0,a),利用向量的夹角公式,可得结论;
=(0,0,a),利用向量的夹角公式,可得结论;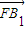 为平面BCC1B1的法向量,求出平面FCC1的法向量,利用向量的夹角公式,可得结论.
为平面BCC1B1的法向量,求出平面FCC1的法向量,利用向量的夹角公式,可得结论.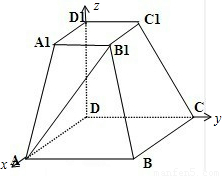 解;依题意知,该多面体为底面是正方形的四棱台,且D1D⊥底面ABCD,AB=2A1B1=2DD1=2a…(2分)
解;依题意知,该多面体为底面是正方形的四棱台,且D1D⊥底面ABCD,AB=2A1B1=2DD1=2a…(2分) =(-a,a,a),
=(-a,a,a), =(0,0,a)
=(0,0,a) >=
>= =
=
 …(6分)
…(6分) =(-a,a,a),
=(-a,a,a), =(-2a,0,0),
=(-2a,0,0), =(a-x,a,a-z)
=(a-x,a,a-z)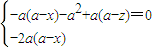 得
得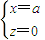
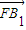 为平面BCC1B1的法向量.
为平面BCC1B1的法向量. =(x1,y1,z,)为平面FCC1的法向量.
=(x1,y1,z,)为平面FCC1的法向量. =(0,-a,a),
=(0,-a,a), =)-a,2a,0)
=)-a,2a,0)
 =(2,1,1)
=(2,1,1) >=
>=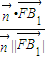 =
=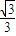
 …(12分)
…(12分)

科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年日照质检理)(12分)
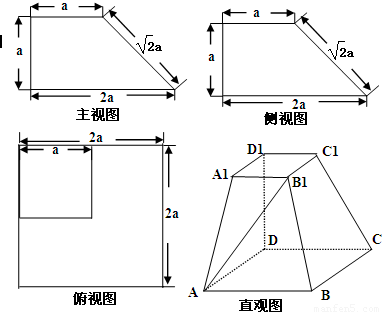
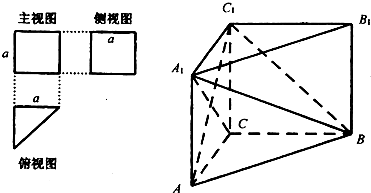
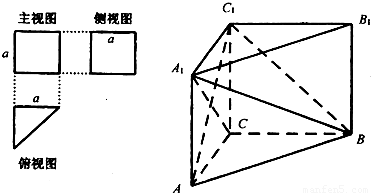
一个多面体的三视图及直观图如图所示,其中主视图和左视图都是边长为2的正方形,俯视图是腰长为2的等腰直角三角形,M、N分别是A1B、B1C1的中点。
(I)求证:MN⊥平面A1BC;
(II)求异面直线AM和CA1所成的角的大小;
(III)求二面角A―A1B―C的大小。
|
查看答案和解析>>
科目:高中数学 来源:2010年天津市河西区高考数学二模试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com