
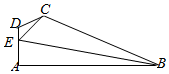
 如图,在平面四边形ABCD中,DA⊥AB,DE=2,EC=$\sqrt{7}$,EA=3,∠ADC=$\frac{2π}{3}$,∠BEC=$\frac{π}{2}$.
如图,在平面四边形ABCD中,DA⊥AB,DE=2,EC=$\sqrt{7}$,EA=3,∠ADC=$\frac{2π}{3}$,∠BEC=$\frac{π}{2}$.分析 (1)在△CDE中,由余弦定理,即可求得CD的值,由正弦定理即可求得sin∠CED的值;
(2)由题意可知cos∠AEB的值,在在Rt△EAB中,cos∠AEB=$\frac{EA}{BE}$,即可求得BE的值.
解答 解:(1)设∠CED=α,在△CDE中,由余弦定理,得EC2=CD2+DE2-2CD•DE•cos∠EDC
于是由题设知,7=CD2+4+2CD,即CD2+2CD-3=0解得CD=1(CD=-3舍去),
在△CDE中,由正弦定理,得$\frac{EC}{sin∠EDC}=\frac{CD}{α}$,
$sinα=\frac{{CD•\frac{2π}{3}}}{EC}=\frac{{\frac{{\sqrt{3}}}{2}}}{{\sqrt{7}}}=\frac{{\sqrt{21}}}{14},即sin∠CED=\frac{{\sqrt{21}}}{14}$;…(6分)
(2)由题设知,$0<α<\frac{π}{2}$,于是由(1)知,
而$∠AEB=\frac{π}{2}-α$,所以$cos∠AEB=\frac{{\sqrt{21}}}{14}$
在Rt△EAB中,$cos∠AEB=\frac{EA}{BE}=\frac{3}{BE}=\frac{{\sqrt{21}}}{14}$,
∴$BE=2\sqrt{21}$.…(12分)
点评 本题主要考查解三角形的应用,根据正弦定理和余弦定理是解决本题本题的关键,难度不大,属于中档题.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:解答题
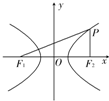 如图,已知F1、F2为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点,过F2作垂直于x轴的直线交双曲线于点P,且∠PF1F2=30°.求:
如图,已知F1、F2为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点,过F2作垂直于x轴的直线交双曲线于点P,且∠PF1F2=30°.求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com