
分析 (1)由条件求得f(x)=|2x-a|≥5的解集,再根据它的解集为{x|x≤-2或x≥3},求得a的值.
(2)由题意可得|x+1|+|2x-a|≥1 恒成立.设g(x)=|x+1|+|2x-a|,则g(x)min≥1.分类讨论,求得g(x)的最小值,可得a的范围.
解答 解:(1)根据函数f(x)=|2x-a|≥5,可得 2x-a≥5,或2x-a≤-5,
求得它的解集为{x|x≥$\frac{a+5}{2}$,或x≤$\frac{a-5}{2}$}.
再根据它的解集为{x|x≤-2或x≥3},可得$\frac{a+5}{2}$=3,且 $\frac{a-5}{2}$=-2,求得a=1.
(2)若f(x)≥1-|x+1|恒成立,则|x+1|+|2x-a|≥1 恒成立.
设g(x)=|x+1|+|2x-a|,由题意可得,g(x)min≥1.
①当$\frac{a}{2}$<-1时,即a<-2时,g(x)=$\left\{\begin{array}{l}{a-1-3x,x<\frac{a}{2}}\\{x-a-1,\frac{a}{2}≤x≤-1}\\{3x+1-a,x≥-1}\end{array}\right.$,由单调性求得g(x)的最小值为g($\frac{a}{2}$)=-$\frac{a}{2}$-1,
∴-$\frac{a}{2}$-1≥1,求得a≤-4,故此时,a的范围为{a|a≤-4 }.
②当$\frac{a}{2}$>-1时,即a>-2时,g(x)=$\left\{\begin{array}{l}{a-1-3x,x<-1}\\{a+1-x,-1≤x≤\frac{a}{2}}\\{3x+1-a,x>\frac{a}{2}}\end{array}\right.$,由单调性求得g(x)的最小值为g($\frac{a}{2}$)=$\frac{a}{2}$+1,
∴$\frac{a}{2}$+1≥1,求得a≥0,故此时,a的范围为∅.
③当$\frac{a}{2}$=-1时,即a=-2时,g(x)=3|x+1|≥0,不满足g(x)min≥1.
综上可得,a的范围为{a|a≤-4 }.
点评 本题主要考查绝对值不等式的解法,函数的恒成立问题,利用单调性求函数的最值,属于中档题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:解答题
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{6}{125}$ | a | b | $\frac{24}{125}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
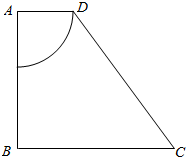 如图所示,在直角梯形ABCD 中,已知AB=4,BC=5,AD=2,以顶点A 为圆心,AD 为半径剪去一个扇形,剩下的部分绕AB 旋转一周形成一个几何体,指出该几何体的结构特征,并求该几何体的体积V 和表面积S.
如图所示,在直角梯形ABCD 中,已知AB=4,BC=5,AD=2,以顶点A 为圆心,AD 为半径剪去一个扇形,剩下的部分绕AB 旋转一周形成一个几何体,指出该几何体的结构特征,并求该几何体的体积V 和表面积S.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com