
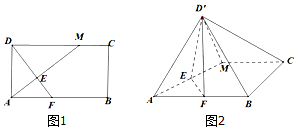
 如图,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C,得四棱锥D′-ABCM.
如图,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C,得四棱锥D′-ABCM.分析 (1)由题意可知,AM⊥D′E,AM⊥EF,利用线面垂直的判定可得AM⊥平面D′EF,进一步得到平面D′EF⊥平面AMCB;
(2)过D′作D′H⊥EF于H,由平面D′EF⊥平面AMCB,可得D′H⊥平面AMCB,得到∠D′FE=$\frac{π}{3}$,结合∠D′EF=$\frac{π}{3}$,可得△D′FE是正三角形.然后求解直角三角形可得D′H,利用等积法求得几何体A-D′EF的体积.
解答 (1)证明:∵AM⊥D′E,AM⊥EF,且D′E∩EF=E,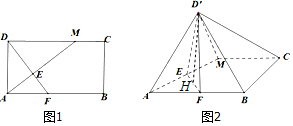
∴AM⊥平面D′EF,
∵AM?平面AMCB,
∴平面D′EF⊥平面AMCB;
(2)解:过D′作D′H⊥EF于H,
∵平面D′EF⊥平面AMCB,
∴D′H⊥平面AMCB,
∵直线D′F与平面ABCM所成角的大小为$\frac{π}{3}$,
∴∠D′FE=$\frac{π}{3}$,又∠D′EF=$\frac{π}{3}$,则△D′FE是正三角形.
∵AB=2BC=4,
∴AD=DF=2,EF=$\sqrt{2}$,
∴D′H=$\frac{\sqrt{6}}{2}$,S△AEF=1,
则${V}_{A-D′EF}={V}_{D′-AEF}=\frac{1}{3}×1×\frac{\sqrt{6}}{2}=\frac{\sqrt{6}}{6}$.
点评 本题考查平面与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


科目:高中数学 来源: 题型:填空题
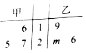 甲、乙两组数据的茎叶图如图所示,其中m为小于10的自然数,已知甲组数据的中位数大于乙组数据的中位数,则甲组数据的平均数也大于乙组数据的平均数的概率为$\frac{3}{5}$.
甲、乙两组数据的茎叶图如图所示,其中m为小于10的自然数,已知甲组数据的中位数大于乙组数据的中位数,则甲组数据的平均数也大于乙组数据的平均数的概率为$\frac{3}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
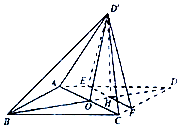 如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=EF,EF交BD于点H,将△DEF沿EF折到△D'EF的位置.
如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=EF,EF交BD于点H,将△DEF沿EF折到△D'EF的位置.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
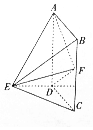 在多面体ABCDE中,ABCD是矩形,平面ABCD⊥平面CDE,CD⊥DE,2DE=2DC=BC,F是棱BC的中点.
在多面体ABCDE中,ABCD是矩形,平面ABCD⊥平面CDE,CD⊥DE,2DE=2DC=BC,F是棱BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{50}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个正面和最多一个正面 | B. | 最多两个正面和至少两个正面 | ||
| C. | 不多于一个正面和至少两个正面 | D. | 至少两个正面和恰有一个正面 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com