
分析 先根据二倍角公式化简被积函数,再根据定积分的计算法则计算即可.
解答 解:$\frac{cos2x}{cosx+sinx}$dx=$\frac{co{s}^{2}x-si{n}^{2}x}{cosx+sinx}$=cosx-sinx,
∴${∫}_{0}^{\frac{π}{4}}$$\frac{cos2x}{cosx+sinx}$dx=${∫}_{0}^{\frac{π}{4}}$(cosx-sinx)dx=(sinx+cosx)|${\;}_{0}^{\frac{π}{4}}$=(sin$\frac{π}{4}$+cos$\frac{π}{4}$)-(sin0+cos0)=$\sqrt{2}$-1,
故答案为:$\sqrt{2}$-1
点评 本题考查了定积分的计算,关键是求出原函数,属于基础题.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:| A. | ①④ | B. | ②④ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
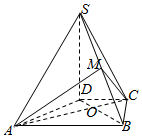 如图所示,四棱锥S-ABCD的底面ABCD为等腰梯形,CD∥AB,AC⊥BD,垂足为O,侧面SAD⊥底面ABCD,且∠ADS=$\frac{π}{2}$,AB=8,AD=$\sqrt{34}$,SD=$\sqrt{30}$,M为BS中点.
如图所示,四棱锥S-ABCD的底面ABCD为等腰梯形,CD∥AB,AC⊥BD,垂足为O,侧面SAD⊥底面ABCD,且∠ADS=$\frac{π}{2}$,AB=8,AD=$\sqrt{34}$,SD=$\sqrt{30}$,M为BS中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | -$\frac{1}{3}$ | C. | -$\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com