
【题目】为了迎接2000年的到来,某地组织了一次乒乓球迎春幸运赛.首先,通过身份号抽选出2000名选手,编号为1,2,…,2000,他们当中任两人都可以组成一对双打选手,每对选手的编号之和称为他们的“和号”.规定:“和号”相同的两对选手方有资格进行幸运双打赛.比赛开始前,组委会首先从2000个编号中随机抽出65名幸运选手,然后找出“和号”相同的两对选手进行幸运双打赛(凡同一“和号”的选手分在同一区进行单循环).求证:无论怎样抽选,总有选手进行幸运赛.
【答案】见解析
【解析】
因从1~2000两两作差(这里规定大数减小数),只有从1~1999共1999个数(作l999个抽屉).
而任取65个编号![]() (规定
(规定![]() )两两作差(大数减小数),可得
)两两作差(大数减小数),可得![]() 个差(作2080个苹果).
个差(作2080个苹果).
由抽屉原理知,必存在差相等的情况.下面就差相等的个数进行讨论.
(1)若2080个差中,存在3个差相等的情况.设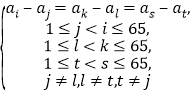
(i)若![]() ,则
,则![]() 与
与![]() 配对,
配对,![]() 与
与![]() 配对,可进行幸运赛.
配对,可进行幸运赛.
(ii)若![]() (称为相邻等差对),则
(称为相邻等差对),则![]() ,从而
,从而![]() 与
与![]() 配对,
配对,![]() 与
与![]() 配对,可进行幸运赛.
配对,可进行幸运赛.
(2)若2080个差中,不存在有3个差相等的情况,此时,由![]() 知,两个差相等的情况至少发生了81次.
知,两个差相等的情况至少发生了81次.
考虑这些相等差: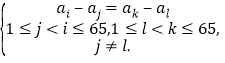 ①
①
(i)若![]() 的情况不超过64次,则81个棚等差中必存在
的情况不超过64次,则81个棚等差中必存在![]() ,使式①成立.此时
,使式①成立.此时![]() 与
与![]() ,配对,
,配对,![]() 与
与![]() 配对,可进行幸运赛.
配对,可进行幸运赛.
(ii)若![]() 的情况至少发生64次,由于此时的
的情况至少发生64次,由于此时的![]() 只能取
只能取![]() 共63个值,故必有关于
共63个值,故必有关于![]() 的相邻等差对重复出现.即存在
的相邻等差对重复出现.即存在![]() ,
,![]() 使
使![]()
相减得![]() .
.
即![]() 与
与![]() 配对,
配对,![]() 与
与![]() 配对,可进行幸运赛.
配对,可进行幸运赛.
综上得,随机抽出65名选手,总可进行幸运赛.


科目:高中数学 来源: 题型:
【题目】函数f(x)=ax3+3x2+3x(a≠0).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)在区间(1,2)是增函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆C:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,直线l:
,直线l:![]() 与椭圆C交于A,B两点
与椭圆C交于A,B两点![]() 为坐标原点.
为坐标原点.
![]() 若直线l过点
若直线l过点![]() ,且
,且![]() 十
十![]() ,求直线l的方程;
,求直线l的方程;
![]() 若以AB为直径的圆过点O,点P是线段AB上的点,满足
若以AB为直径的圆过点O,点P是线段AB上的点,满足![]() ,求点P的轨迹方程.
,求点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆C:![]() 的左右焦点分别为F1,F2,直线l:y=kx+m与椭圆C交于A,B两点.O为坐标原点.
的左右焦点分别为F1,F2,直线l:y=kx+m与椭圆C交于A,B两点.O为坐标原点.
(1)若直线l过点F1,且|AB|=![]() ,求k的值;
,求k的值;
(2)若以AB为直径的圆过原点O,试探究点O到直线AB的距离是否为定值?若是,求出该定值;若不是,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,|PQ|=|PA|成立,如图.
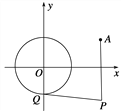
(1)求a,b间的关系;
(2)求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于![]() 分的选手定为合格选手,直接参加第二轮比赛,大于等于
分的选手定为合格选手,直接参加第二轮比赛,大于等于![]() 分的选手将直接参加竞赛选拔赛.已知成绩合格的
分的选手将直接参加竞赛选拔赛.已知成绩合格的![]() 名参赛选手成绩的频率分布直方图如图所示,其中
名参赛选手成绩的频率分布直方图如图所示,其中![]() 的频率构成等比数列.
的频率构成等比数列.
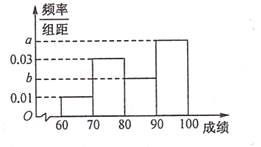
(1)求![]() 的值;
的值;
(2)估计这![]() 名参赛选手的平均成绩;
名参赛选手的平均成绩;
(3)根据已有的经验,参加竞赛选拔赛的选手能够进入正式竞赛比赛的概率为![]() ,假设每名选手能否通过竞赛选拔赛相互独立,现有
,假设每名选手能否通过竞赛选拔赛相互独立,现有![]() 名选手进入竞赛选拔赛,记这
名选手进入竞赛选拔赛,记这![]() 名选手在竞赛选拔赛中通过的人数为随机变量
名选手在竞赛选拔赛中通过的人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.

(Ⅰ)求证:AF∥平面PEC;
(Ⅱ)求证:平面PEC⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,右顶点为
,右顶点为![]() ,且
,且![]() 过点
过点![]() ,圆
,圆![]() 是以线段
是以线段![]() 为直径的圆,经过点
为直径的圆,经过点![]() 且倾斜角为
且倾斜角为![]() 的直线与圆
的直线与圆![]() 相切.
相切.
(1)求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
(2)是否存在直线![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相切,与椭圆
相切,与椭圆![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ?若存在,请求出直线
?若存在,请求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com