
已知曲线 (
( 为参数),曲线
为参数),曲线 ,将
,将 的横坐标伸长为原来的2倍,纵坐标缩短为原来的
的横坐标伸长为原来的2倍,纵坐标缩短为原来的 得到曲线
得到曲线 .
.
(1)求曲线 的普通方程,曲线
的普通方程,曲线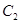 的直角坐标方程;
的直角坐标方程;
(2)若点P为曲线 上的任意一点,Q为曲线
上的任意一点,Q为曲线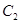 上的任意一点,求线段
上的任意一点,求线段 的最小值,并求此时的P的坐标.
的最小值,并求此时的P的坐标.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
在直角坐标平面内,以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线 的极坐标方程为
的极坐标方程为 ,直线
,直线 的参数方程为
的参数方程为 (
( 为参数).
为参数).
(1)分别求出曲线 和直线
和直线 的直角坐标方程;
的直角坐标方程;
(2)若点 在曲线
在曲线 上,且
上,且 到直线
到直线 的距离为1,求满足这样条件的点
的距离为1,求满足这样条件的点 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分) 直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的方程为
 ,直线
,直线 方程为
方程为 (t为参数),直线
(t为参数),直线 与C的公共点为T.
与C的公共点为T.
(1)求点T的极坐标;
(2)过点T作直线 ,
, 被曲线C截得的线段长为2,求直线
被曲线C截得的线段长为2,求直线 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知直线C1: (t为参数),C2:
(t为参数),C2: (θ为参数).
(θ为参数).
(1)当α= 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;
(2)过坐标原点O作C1的垂线,垂足为A,P为OA中点,当α变化时,求P点的轨迹的参数方程,并指出它是什么曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知曲线 的参数方程是
的参数方程是 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线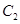 的极坐标方程是
的极坐标方程是 .
.
(1)写出 的极坐标方程和
的极坐标方程和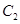 的直角坐标方程;
的直角坐标方程;
(2)已知点 、
、 的极坐标分别是
的极坐标分别是 、
、 ,直线
,直线 与曲线
与曲线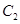 相交于
相交于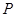 、
、 两点,射线
两点,射线 与曲线
与曲线 相交于点
相交于点 ,射线
,射线 与曲线
与曲线 相交于点
相交于点 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知曲线C:ρsin(θ+ )=
)= ,曲线P:ρ2-4ρcosθ+3=0,
,曲线P:ρ2-4ρcosθ+3=0,
(1)求曲线C,P的直角坐标方程.
(2)设曲线C和曲线P的交点为A,B,求|AB|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com