Question

直线l过点P（0，-2），按下列条件求直线l的方程
（1）直线l与两坐标轴围成三角形面积为4；
（2）直线l与线段AB有公共点（包括线段两端点），且A（1，2）、B（-4，1），求直线l斜率k的取值范围．

Answer 1

分析：（1）设直线l方程的斜率为k，由过P表示出直线l的方程，分别令x和y等于0求出与两坐标轴的交点，利用三角形的面积公式表示出与坐标轴围成三角形的面积，让其值等于4列出关于k的方程，求出方程的解即可得到k的值，从而确定出直线l的方程；
（2）由直线l恒过P（0，-2），由A，B及P的坐标分别求出直线PA和直线PB方程的斜率，根据直线l与线段AB有公共点，结合图形，由求出的两斜率即可得到k的取值范围．

解答：解：（1）设直线l方程为：y=kx-2（1分）
则直线l与两坐标轴交点分别为(

2

k

，0)，（0，-2）（3分）
∴围成三角形面积为

1

2

•|

2

k

|•2=4（5分）
∴k=±

1

2

，
∴直线l方程为x+2y+4=0或x-2y-4=0；（7分）
（2）由直线方程y=kx-2可知直线过定点P（0，-2），
∵kPB=

1-(-2)

(-4)-0

=-

3

4

，kPA=

2-(-2)

1-0

=4，（11分）
∴要使直线l与线段PQ有交点，则k的取值范围是k≥4或k≤-

3

4

．（14分）

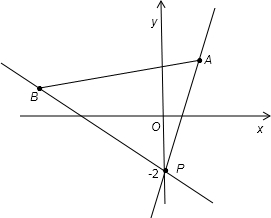
点评：此题考查了直线的截距式方程，以及直线的图象特征与倾斜角、斜率的关系．学生作第二问时，求出特殊位置时的斜率的值，借助图形写出k的取值范围，考查了学生利用数形结合的思想解决问题的能力．