
【题目】已知函数f(x)=lg(![]() )(a>1>b>0).
)(a>1>b>0).
(1)求函数y=f(x)的定义域;
(2)在函数y=f(x)的图象上是否存在不同的两点,使过此两点的直线平行于x轴;
(3)当a、b满足什么关系时,f(x)在区间![]() 上恒取正值.
上恒取正值.
【答案】(1)![]() ;(2)不存在;(3)
;(2)不存在;(3)![]() .
.
【解析】
试题分析:(1)由![]()
![]()
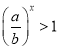 ,又
,又![]()
![]()
![]()
![]()
![]()
![]()
![]() 的定义域为
的定义域为![]() ;(2)设
;(2)设![]() ,由
,由![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 在区间
在区间![]() 上是增函数.假设函数
上是增函数.假设函数![]() 的图象上存在不同的两点
的图象上存在不同的两点![]() 、
、![]() ,使得直线
,使得直线![]() 平行于
平行于![]() 轴,即
轴,即![]() ,
,![]() ,这与
,这与![]() 是增函数矛盾
是增函数矛盾![]() 函数
函数![]() 的图象上不存在不同的两点,使过此两点的直线平行于
的图象上不存在不同的两点,使过此两点的直线平行于![]() 轴;(3)由(2)知,
轴;(3)由(2)知,![]() 在区间
在区间![]() 上是增函数
上是增函数![]() 当
当![]() 时,
时,![]()
![]() 只需
只需![]()
![]()
![]()
![]()
![]()
![]()
![]() 时,
时,![]() 在区间
在区间![]() 上恒取正值.
上恒取正值.
试题解析: (1)由![]() ,得
,得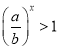 ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,即函数
,即函数![]() 的定义域为
的定义域为![]() .
.
(2)设![]() ,因为
,因为![]() ,所以
,所以![]() ,
,![]() ,则
,则![]() ,所以
,所以![]() ,于是
,于是![]() ,即
,即![]() ,因此函数
,因此函数![]() 在区间
在区间![]() 上是增函数.假设函数
上是增函数.假设函数![]() 的图象上存在不同的两点
的图象上存在不同的两点![]() 、
、![]() ,使得直线
,使得直线![]() 平行于
平行于![]() 轴,即
轴,即![]() ,
,![]() ,这与
,这与![]() 是增函数矛盾.故函数
是增函数矛盾.故函数![]() 的图象上不存在不同的两点,使过此两点的直线平行于
的图象上不存在不同的两点,使过此两点的直线平行于![]() 轴.
轴.
(3)由(2)知,![]() 在区间
在区间![]() 上是增函数,所以当
上是增函数,所以当![]() 时,
时,![]() ,故只需
,故只需![]() ,即
,即![]() ,即
,即![]() ,所以当
,所以当![]() 时,
时,![]() 在区间
在区间![]() 上恒取正值.
上恒取正值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】对于定义在区间![]() 上的函数
上的函数![]() ,若存在闭区间
,若存在闭区间![]() 和常数
和常数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,且对任意
,且对任意![]() ,当
,当![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 为区间
为区间![]() 上的“平底型”函数.
上的“平底型”函数.
(1)判断函数![]() 和
和![]() 是否为
是否为![]() 上的“平底型”函数?
上的“平底型”函数?
(2)若函数![]() 是区间
是区间![]() 上的“平底型”函数,求
上的“平底型”函数,求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 和
和![]() 分别是
分别是![]() 上的奇函数和偶函数,且
上的奇函数和偶函数,且![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)当![]() 时,分别求出曲线
时,分别求出曲线![]() 和
和![]() 切线斜率的最小值;
切线斜率的最小值;
(Ⅲ)设![]() ,证明:当
,证明:当![]() 时,曲线
时,曲线![]() 在曲线
在曲线![]() 和
和![]() 之间,且相互之间没有公共点.
之间,且相互之间没有公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若p,q为简单命题,则“p且q为假”是“p或q为假”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,且a2=2b.
,且a2=2b.
(1)求椭圆的方程;
(2)直线l:x﹣y+m=0与椭圆交于A,B两点,是否存在实数m,使线段AB的中点在圆x2+y2=5上,若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全国人民代表大会在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和14名女记者担任对外翻译工作.调查发现,男、女记者中分别有10人和6人会俄语.
(1)根据以上数据完成以下![]() 列联表:
列联表:
会俄语 | 不会俄语 | 总计 | |
男 | |||
女 | |||
总计 |
(2)能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5),变量U与V相对应的一组数据为 (10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r1表示变量Y与X之间的线性相关系数,r2表示变量V与U之间的线性相关系数,则( )
A.r2<r1<0 B.0<r2<r1
C.r2<0<r1 D.r2=r1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某加工厂用某原料由车间加工出 产品,由乙车间加工出 产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克 产品,每千克 产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克 产品,每千克 产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天获利最大的生产计划为( )
A. 甲车间加工原料10箱,乙车间加工原料60箱
B. 甲车间加工原料15箱,乙车间加工原料55箱
C. 甲车间加工原料18箱,乙车间加工原料50箱
D. 甲车间加工原料40箱,乙车间加工原料30箱
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com