
分析 (I)由题意可知:${a_{n+1}}={a_n}^2+2{a_n}$,${a_{n+1}}+1={a_n}^2+2{a_n}+1=({a_n}+1{)^2}$,两边取对数,即可求得bn+1=2bn,则{bn}是以2为公比的等比数列,利用等比数列通项公式即可求得an,代入即可求得an;
(II)利用数学归纳法即可求证1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{b}_{n}-1}$<n(n≥2);
(III).证明:由${2^{c_n}}={b_n}$得cn=n,${(\frac{{{c_{n+1}}}}{c_n})^n}={(\frac{1+n}{n})^n}={(1+\frac{1}{n})^n}$,利用二项式定理展开,${(1+\frac{1}{n})^n}=C_n^0+C_n^1\frac{1}{n}+C_n^2\frac{1}{n^2}+…+C_n^k\frac{1}{n^k}+…+C_n^n\frac{1}{n^n}$$<1+1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…\frac{1}{n-1}-\frac{1}{n}=3-\frac{1}{n}<3$,当n=1时显然成立.所以得证.
解答 解:(I)由${a_{n+1}}={a_n}^2+2{a_n}$,则${a_{n+1}}+1={a_n}^2+2{a_n}+1=({a_n}+1{)^2}$,
由a1=3,则an>0,两边取对数得到${log_2}({a_{n+1}}+1)={log_2}({a_n}+1{)^2}=2{log_2}({a_n}+1)$,即bn+1=2bn(2分)
又b1=log2(a1+1)=2≠0,
∴{bn}是以2为公比的等比数列.
即${b_n}={2^n}$(3分)
又∵bn=log2(an+1),
∴${a_n}={2^{2^n}}-1$(4分)
(2)用数学归纳法证明:1o当n=2时,左边为$1+\frac{1}{2}+\frac{1}{3}=\frac{11}{6}<2$=右边,此时不等式成立; (5分)
2o假设当n=k≥2时,不等式成立,
则当n=k+1时,左边=$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{{{2^k}-1}}+\frac{1}{2^k}+\frac{1}{{{2^k}+1}}+…\frac{1}{{{2^{k+1}}-1}}$(6分)
$<k+\frac{1}{2^k}+\frac{1}{{{2^k}+1}}+…\frac{1}{{{2^{k+1}}-1}}$$<k+\overbrace{\frac{1}{2^k}+\frac{1}{2^k}+…\frac{1}{2^k}}^{{2^k}个}$<k+1=右边
∴当n=k+1时,不等式成立.
综上可得:对一切n∈N*,n≥2,命题成立.(9分)
(3)证明:由${2^{c_n}}={b_n}$得cn=n,
∴${(\frac{{{c_{n+1}}}}{c_n})^n}={(\frac{1+n}{n})^n}={(1+\frac{1}{n})^n}$,
首先${(1+\frac{1}{n})^n}=C_n^0+C_n^1\frac{1}{n}+C_n^2\frac{1}{n^2}+…+C_n^k\frac{1}{n^k}+…+C_n^n\frac{1}{n^n}≥2$,(10分)
其次∵$C_n^k\frac{1}{n^k}=\frac{n(n-1)…(n-k+1)}{{k!{n^k}}}<\frac{1}{k!}≤\frac{1}{k(k-1)}=\frac{1}{k-1}-\frac{1}{k}(k≥2)$,
∴${(1+\frac{1}{n})^n}=C_n^0+C_n^1\frac{1}{n}+C_n^2\frac{1}{n^2}+…+C_n^k\frac{1}{n^k}+…+C_n^n\frac{1}{n^n}$,
$<1+1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…\frac{1}{n-1}-\frac{1}{n}=3-\frac{1}{n}<3$,
当n=1时显然成立.所以得证.(15分)
点评 本题考查等比数列通项公式,对数的运算性质,考查数学归纳法求证不等式成立,二项式定理,考查计算能力,属于难题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| 储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 将图象上的每一点横坐标缩短到原来的$\frac{1}{2}$而纵坐标不变 | |
| B. | 沿x向左平移$\frac{π}{2}$个单位,再把得图象上的每一点横坐标伸长到原来的2而纵坐标不变 | |
| C. | 先把图象上的每一点横坐标缩短到原来的$\frac{1}{2}$而纵坐标不变,再将所得图象沿x向右平移$\frac{π}{4}$个单位 | |
| D. | 先把图象上的每一点横坐标缩短到原来的$\frac{1}{2}$而纵坐标不变,再将所得图象沿x向左平移$\frac{π}{2}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,四边形ABCD为矩形,AB⊥BP,M为AC的中点,N为PD上一点.
如图,在四棱锥P-ABCD中,四边形ABCD为矩形,AB⊥BP,M为AC的中点,N为PD上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
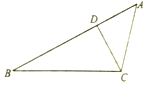 如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.
如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)<ef(0),f(2017)>e2017f(0) | B. | f(1)>ef(0),f(2017)>e2017f(0) | ||
| C. | f(1)>ef(0),f(2017)<e2017f(0) | D. | f(1)<ef(0),f(2017)<e2017f(0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com