
(08年长郡中学一模理)如图,设![]() 是椭圆
是椭圆![]() 的左焦点,直线
的左焦点,直线![]() 为对应的准线,直线
为对应的准线,直线![]() 与
与![]() 轴交于
轴交于![]() 点,
点,![]() 为椭圆的长轴,已知
为椭圆的长轴,已知![]() ,且
,且![]() .
.
(1)求椭圆的标准方程;
(2)求证:对于任意的割线![]() ,恒有
,恒有![]() ;
;
(3)求三角形△ABF面积的最大值.

科目:高中数学 来源: 题型:
(08年长郡中学一模理)(12分) 在北京友好运动会中,甲、乙、丙三名选手进行单循环赛(即每两人比赛一场),共赛三场,每场比赛胜者得1分,输者得0分,没有平局;在每一场比赛中,甲胜乙的概率为![]() ,甲胜丙的概率为
,甲胜丙的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() .
.
(Ⅰ)求甲获得小组第一且丙获得小组第二的概率;
(Ⅱ)求三人得分相同的概率;
(Ⅲ)设在该小组比赛中甲得分数为![]() ,求Eξ.
,求Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
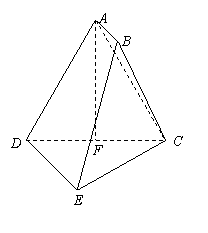
(08年长郡中学一模理)(12分)已知在多面体ABCDE中,AB⊥平面ACD,DE∥AB,AC = AD = CD = DE = 2,
F为CD的中点.
(Ⅰ)求证:AF⊥平面CDE;
(Ⅱ)求平面ABC和平面CDE所成的小于90°的二面角的大小;
(Ⅲ)求点A到平面BCD的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年长郡中学一模理)(13分)某中学有教职员工500人,为了开展迎2008奥运全民健身活动,增强教职员工体质,学校工会鼓励大家积极参加晨练与晚练,每天清晨与晚上定时开放运动场、健身房和乒乓球室,约有30%的教职员工坚持每天锻炼. 据调查统计,每次去户外锻炼的人有10%下次去室内锻炼,而在室内锻炼的人有20%下次去户外锻炼. 请问,随着时间的推移,去户外锻炼的人数能否趋于稳定?稳定在多少人左右?
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年长郡中学一模文)(12分)如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面![]() 内作菱形ABCD,边长为1,∠BAD=60°,再在面
内作菱形ABCD,边长为1,∠BAD=60°,再在面![]() 的上方,分别以△
的上方,分别以△![]() 与△
与△![]() 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
(Ⅰ)求证:PQ⊥BD;
(Ⅱ)求二面角P-BD-Q的余弦值;
(Ⅲ)求点P到平面QBD的距离;

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年长郡中学一模文)(13分)已知函数![]() ,
,
①若![]() 在区间
在区间![]() 上单调递减,求实数
上单调递减,求实数![]() 的取值范围。
的取值范围。
②若过点![]() 可作函数
可作函数![]() 图象的三条切线,求实数
图象的三条切线,求实数![]() 的取值范围。
的取值范围。
③设点![]() ,
,![]() ,记点
,记点![]() ,求证:在区间
,求证:在区间![]() 内至少有一实数
内至少有一实数![]() ,使得函数
,使得函数![]() 图象在
图象在![]() 处的切线平行于直线
处的切线平行于直线![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com