
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,且
为参数,且![]() ),以
),以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线 ![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若曲线![]() 与
与![]() 只有一个公共点,求
只有一个公共点,求![]() 的值;
的值;
(2)![]() ,
, ![]() 为曲线
为曲线![]() 上的两点,且
上的两点,且![]() ,求△
,求△![]() 的面积最大值.
的面积最大值.
【答案】(1)a=1;(2)见解析.
【解析】试题分析:(1)根据曲线![]() 的参数方程可得曲线
的参数方程可得曲线![]() 是以
是以![]() 为圆心,以
为圆心,以![]() 为半径的圆,再将直线
为半径的圆,再将直线![]() 的极坐标方程化为直角坐标方程,根据曲线
的极坐标方程化为直角坐标方程,根据曲线![]() 与
与![]() 只有一个公共点,由圆心到直线的距离等于半径,即可求得
只有一个公共点,由圆心到直线的距离等于半径,即可求得![]() 的值;(2)法一:由题意,曲线
的值;(2)法一:由题意,曲线![]() 的极坐标方程为
的极坐标方程为![]() 设
设![]() 的极角为
的极角为![]() ,
, ![]() 的极角为
的极角为![]() ,即可表示出
,即可表示出![]() ,根据积化和差公式及三角函数图象即可求得△
,根据积化和差公式及三角函数图象即可求得△![]() 的面积最大值;法二:根据曲线
的面积最大值;法二:根据曲线![]() 是圆及
是圆及![]() ,利用正弦定理可得
,利用正弦定理可得![]() ,再根据余弦定理与基本不等式即可求得
,再根据余弦定理与基本不等式即可求得![]() 的最大值,从而可得△
的最大值,从而可得△![]() 的面积最大值.
的面积最大值.
试题解析:(1)由题意可得曲线![]() 是以
是以![]() 为圆心,以
为圆心,以![]() 为半径的圆;
为半径的圆;
直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
由直线![]() 与圆
与圆![]() 只有一个公共点,则可得
只有一个公共点,则可得![]() .
.
∴![]() (舍)或
(舍)或![]()
∴![]()
(2)法一:由题意,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
设![]() 的极角为
的极角为![]() ,
, ![]() 的极角为
的极角为![]() ,则:
,则: ![]()
∵![]()
∴当![]() 时,
时, ![]() 取得最大值为
取得最大值为![]() .
.
∴![]() 的面积最大值为
的面积最大值为![]() .
.
法二:∵曲线![]() 是以
是以![]() 为圆心,以
为圆心,以![]() 为半径的圆,且
为半径的圆,且![]() .
.
∴由正弦定理得: 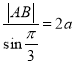 ,即
,即![]() .
.
∴由余弦定理得: ![]() ,则:
,则: ![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
∴![]() 的面积最大值为
的面积最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,卷一《方田》中有如下两个问题:
[三三]今有宛田,下周三十步,径十六步.问为田几何?
[三四]又有宛田,下周九十九步,径五十一步.问为田几何?
翻译为:[三三]现有扇形田,弧长30步,直径长16步.问这块田面积是多少?
[三四]又有一扇形田,弧长99步,直径长51步.问这块田面积是多少?
则下列说法正确的是( )
A.问题[三三]中扇形的面积为240平方步B.问题[三四]中扇形的面积为![]() 平方步
平方步
C.问题[三三]中扇形的面积为60平方步D.问题[三四]中扇形的面积为![]() 平方步
平方步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述中正确的是( )
A.若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
B.若三个平面两两相交,其中两个平面的交线与第三个平面平行.则另外两条交线平行;
C.如果![]() 是两条异面直线,那么直线
是两条异面直线,那么直线![]() 一定是异面直线;
一定是异面直线;
D.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 绕
绕![]() 所在直线旋转一周,所形成的几何体的轴截面面积为10.
所在直线旋转一周,所形成的几何体的轴截面面积为10.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,M、N分别是AB、BC的中点.

(1)求证:MN∥平面A1B1C1D1
(2)求证:平面B1MN⊥平面BB1D1D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() .
.
⑴ 求证:数列![]() 为等差数列;
为等差数列;
⑵ 设![]() ,
, ![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若当
,若当![]() 且
且![]() 为偶数时,
为偶数时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
⑶ 设数列![]() 的前
的前![]() 项的和为
项的和为![]() ,试求数列
,试求数列![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com