
【题目】某同学在上学路上要经过![]() 、
、![]() 、
、![]() 三个带有红绿灯的路口.已知他在
三个带有红绿灯的路口.已知他在![]() 、
、![]() 、
、![]() 三个路口遇到红灯的概率依次是
三个路口遇到红灯的概率依次是![]() 、
、![]() 、
、![]() ,遇到红灯时停留的时间依次是
,遇到红灯时停留的时间依次是![]() 秒、
秒、![]() 秒、
秒、![]() 秒,且在各路口是否遇到红灯是相互独立的.
秒,且在各路口是否遇到红灯是相互独立的.
(1)求这名同学在上学路上在第三个路口首次遇到红灯的概率;,
(2)求这名同学在上学路上因遇到红灯停留的总时间.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)先确定事件:“这名同学在第一和第二个路口没有遇到红灯,在第三个路口遇到红灯”,再根据概率乘法求概率(2)即求数学期望:先确定随机变量取法,再分别求对应概率,最后根据数学期望公式求期望
试题解析:(1)设这名同学在上学路上到第三个路口时首次遇到红灯为事件![]() ,
,
因为事件![]() 等于事件“这名同学在第一和第二个路口没有遇到红灯,在第三个路口遇到红灯” ,
等于事件“这名同学在第一和第二个路口没有遇到红灯,在第三个路口遇到红灯” ,
所以事件![]() 的概率为
的概率为![]() .
.
(2)记“这名同学在上学路上因遇到红灯停留的总时间”为![]() ,
,
由题意,可得![]() 可能取的值为0,40,20,80,60,100,120,140(单位:秒).
可能取的值为0,40,20,80,60,100,120,140(单位:秒).
∴即![]() 的分布列是:
的分布列是:
![]() ;
; ![]() ;
;
![]() ;
;![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]()
所以 .
.
答:这名同学在上学路上因遇到红灯停留的总时间为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,DP⊥x轴,点M在DP的延长线上,且|DM|=2|DP|.当点P在圆x2+y2=1上运动时.
(Ⅰ)求点M的轨迹C的方程;
(Ⅱ)过点T(0,t)作圆x2+y2=1的切线交曲线C于A,B两点,求△AOB面积S的最大值和相应的点T的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图所示的几何体中, ![]() 为三棱柱,且
为三棱柱,且![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() .
.
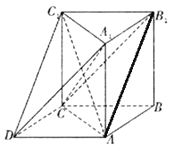
(1)求证: ![]() ;
;
(2)若![]() ,求证:
,求证: ![]() ;
;
(3)若![]() ,二面角
,二面角![]() 的余弦值为若
的余弦值为若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(x2+tx+2)(t为常数,且﹣2 ![]() <t<2
<t<2 ![]() ).
).
(1)当x∈[0,2]时,求函数f(x)的最小值(用t表示);
(2)是否存在不同的实数a,b,使得f(a)=lga,f(b)=lgb,并且a,b∈(0,2).若存在,求出实数t的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数.
上的奇函数.
(1)当![]() 时,
时, ![]() ,若当
,若当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(2)若![]() 的图像关于
的图像关于![]() 对称,且
对称,且![]() 时,
时, ![]() ,求当
,求当![]() 时,
时, ![]() 的解析式;
的解析式;
(3)当![]() 时,
时, ![]() .若对任意的
.若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() .数列
.数列![]() 满足
满足![]() ,
,![]() ,且
,且![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)是否存在正整数![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() (
(![]() )成等差数列,若存在,求出所有满足条件的
)成等差数列,若存在,求出所有满足条件的![]() ,
,![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知任意角θ以x轴非负半轴为始边,若终边经过点P(x0 , y0),且|OP|=r(r>0),定义sicosθ= ![]() ,称“sicosθ”为“正余弦函数”.对于正余弦函数y=sicosx,有同学得到如下结论: ①该函数是偶函数;
,称“sicosθ”为“正余弦函数”.对于正余弦函数y=sicosx,有同学得到如下结论: ①该函数是偶函数;
②该函数的一个对称中心是( ![]() ,0);
,0);
③该函数的单调递减区间是[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z.
],k∈Z.
④该函数的图象与直线y= ![]() 没有公共点;
没有公共点;
以上结论中,所有正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=aln(x2+1)+bx,g(x)=bx2+2ax+b,(a>0,b>0).已知方程g(x)=0有两个不同的非零实根x1 , x2 .
(1)求证:x1+x2<﹣2;
(2)若实数λ满足等式f(x1)+f(x2)+3a﹣λb=0,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四组函数中,表示相等函数的一组是( )
A.f(x)=1,g(x)=x0?
B.f(x)=|x|,g(t)= ![]()
C.f(x)= ![]() ,g(x)=x+1?
,g(x)=x+1?
D.f(x)=lg(x+1)+lg(x﹣1),g(x)=lg(x2﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com