
����Ŀ����IEC�����ʵ繤ίԱ�ᣩ������ʾ��С�ͷ���������ĿͶ�ʽ��٣��ҿ���ǰ�����������ܷ�����Ȼ��ԴӰ�죬��ĿͶ�ʴ���һ�����գ����ݲ��㣬���ܷ�����������£�
���ܷ��� | һ����� | ������� |
ƽ������m/s | 8.5��10 | 6.5��8.5 |
����Ͷ��A��Ŀ���ʽ�Ϊx��x��0����Ԫ��Ͷ��B��Ŀ�ʽ�Ϊy��y��0����Ԫ�����н���ǣ�δ��һ���ڣ�λ��һ�������A��Ŀ����30%�Ŀ�����Ϊ0.6������20%�Ŀ�����Ϊ0.4��λ�ڶ��������B��Ŀ����35%�Ŀ�����Ϊ0.6������10%�Ŀ�������0.1�����ⲻ�Ŀ�������0.3��
��1����Ͷ��A��B��Ŀ������ֱ�Ϊ�κͦǣ���д�������������ǵķֲ��к�����E�Σ�E�ǣ�
��2��ij��˾�ƻ��ò�����100��Ԫ���ʽ�Ͷ����A��B��Ŀ���ҹ�˾Ҫ���A��Ŀ��Ͷ�ʲ��õ���B��Ŀ�����ݣ�1�����������г����У��Թ���һ���������Ŀ��ƽ������֮��z=E��+E�ǵ����ֵ��
���𰸡�
��1���⣺��Ͷ��A��Ŀ���ʽ�Ϊx��x��0����Ԫ��
δ��һ���ڣ�λ��һ�������A��Ŀ����30%�Ŀ�����Ϊ0.6��
����20%�Ŀ�����Ϊ0.4��
��A��ĿͶ������εķֲ��У�
�� | 0.3x | ��0.2x |
P | 0.6 | 0.4 |
��E��=0.18x��0.08x=0.1x��
��Ͷ��B��Ŀ�ʽ�Ϊy��y��0����Ԫ��
δ��һ���ڣ�λ�ڶ��������B��Ŀ����35%�Ŀ�����Ϊ0.6��
����10%�Ŀ�������0.1�����ⲻ�Ŀ�������0.3��
��B��ĿͶ������ǵķֲ��У�
�� | 0.35y | ��0.1y | 0 |
P | 0.6 | 0.1 | 0.3 |
����=0.21y��0.01y=0.2y
��2���⣺������֪x��y�����Լ������Ϊ 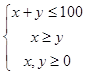 ��
��
�ɣ�1��֪��z=E��+E��=0.1x+0.2y��
��x=50��y=50����zȡ�����ֵ15��
���A��B��Ŀ��Ͷ��50��Ԫ����ʹ��˾�������������������15��Ԫ
����������1������֪���������ø��ʷֲ��е����ʺͼ��㹫ʽ���������������������ǵķֲ��к�����E�Σ�E�ǣ���2���������г�x��y�����Լ���������ɴ˹���һ���������Ŀ��ƽ������֮��z=E��+E�ǵ����ֵ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC����x��1��2+��y��1��2=1�ϴ���4���㵽ֱ��x+y��m=0��m��R���ľ������1�� ![]() ��
��
��1����m��ȡֵ��Χ��
��2���ж�ԲC��ԲD��x2+y2��2mx=0��λ�ù�ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() sin2x��cos2x+1�����н����д�����ǣ� ��
sin2x��cos2x+1�����н����д�����ǣ� ��
A.f��x����ͼ����ڣ� ![]() ��1�����ĶԳ�
��1�����ĶԳ�
B.f��x���ڣ� ![]() ��
�� ![]() ���ϵ����ݼ�
���ϵ����ݼ�
C.f��x����ͼ�����x= ![]() �Գ�
�Գ�
D.f��x�������ֵΪ3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���輯��M={x|x��2}������N={x|0��x��1}�������й�ϵ����ȷ���ǣ� ��
A.M��N=R
B.M��RN=R
C.N��RM=R
D.M��N=M
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Ϊ��ǣ��� ![]() ������
������ ![]() ������{an}������a1=1��an+1=f��an����
������{an}������a1=1��an+1=f��an����
��1������f��x���ı���ʽ��
��2����֤������{an+1}Ϊ�ȱ����У�
��3��������{an}��ǰn���Sn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��ԲO��ֱ����G��AB�ӳ����ϵ�һ�㣬GCD��ԲO�ĸ��ߣ�����G��AG�Ĵ��ߣ���ֱ��AC�ڵ�E����ֱ�� AD�ڵ�F������G��ԲO�����ߣ��е�ΪH�� 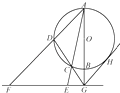
��1����֤��C��D��E��F�ĵ㹲Բ��
��2����GH=8��GE=4����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�ĶԳ�����Ϊ����ԭ��O��������x���ϣ����ҽ���ֱ�ΪF��F�����Ҷ���ֱ�ΪA��B����|F1F2|=4��|AB|=4 ![]()
��1������Բ�ķ��̣�
��2����F1��ֱ��l����ԲC�ཻ��M��N���㣬����MF2N�����Ϊ ![]() ����ֱ��l�ķ��̣�
����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=lnx�� ![]() ��m��R��������[1��e]ȡ����Сֵ4����m= ��
��m��R��������[1��e]ȡ����Сֵ4����m= ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com