
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )
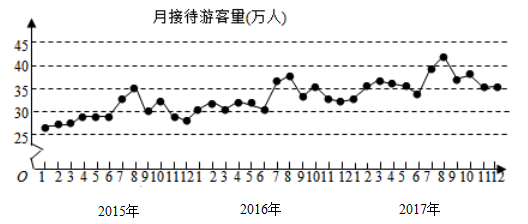
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30万人
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
科目:高中数学 来源: 题型:
【题目】某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在如图所示的6个点A、B、C、A1、、B1、C1上各装一个灯泡,要求同一条线段两端的灯泡不同色,则每种颜色的灯泡都至少用一个的安装方法共有 种(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.已知射线l:θ=![]() 与曲线C:
与曲线C:![]() (t为参数)相交于A,B两点.
(t为参数)相交于A,B两点.
(1)写出射线l的参数方程和曲线C的直角坐标方程;
(2)求线段AB中点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面五边形ABCDE中,AB∥CE,且AE=2,∠AEC=60°,CD=ED=![]() ,cos∠EDC=
,cos∠EDC=![]() .将△CDE沿CE折起,使点D移动到P的位置,且AP=
.将△CDE沿CE折起,使点D移动到P的位置,且AP=![]() ,得到四棱锥P-ABCE.
,得到四棱锥P-ABCE.
(1)求证:AP⊥平面ABCE;
(2)记平面PAB与平面PCE相交于直线l,求证:AB∥l.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一款智能学习APP,学习内容包含文章学习和视频学习两类,且这两类学习互不影响.已知该APP积分规则如下:每阅读一篇文章积1分,每日上限积5分;观看视频累计3分钟积2分,每日上限积6分.经过抽样统计发现,文章学习积分的概率分布表如表1所示,视频学习积分的概率分布表如表2所示.

(1)现随机抽取1人了解学习情况,求其每日学习积分不低于9分的概率;
(2)现随机抽取3人了解学习情况,设积分不低于9分的人数为![]() ,求
,求![]() 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为折痕把
为折痕把![]() 折起,当几何体
折起,当几何体![]() 的的体积最大时,则下列命题中正确的个数是( )
的的体积最大时,则下列命题中正确的个数是( )

①![]()
②![]() ∥平面
∥平面![]()
③![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角
所成的角
④![]() 与
与![]() 所成的角等于
所成的角等于![]() 与
与![]() 所成的角
所成的角
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com