
分析 (1)利用三角函数的诱导公式化简f(x)即可求出f(x)的最小正周期及单调递增区间;
(2)把x-$\frac{π}{12}$代入f(x)化简得$-\frac{{\sqrt{5}}}{2}(sinx+cosx)=(cosx+sinx)(cosx-sinx)$,再分类讨论,当sinx+cosx=0和sinx+cosx≠0时,求出cosx-sinx的值即可.
解答 解:(1)由$f(x)=sinx+cosx•\frac{{\sqrt{3}}}{2}-sinx•\frac{1}{2}$=$\frac{1}{2}sinx+\frac{{\sqrt{3}}}{2}cosx=sin(x+\frac{π}{3})$,
∴f(x)最小正周期T=2π.
由$-\frac{π}{2}+2kπ$≤$x+\frac{π}{3}$≤$\frac{π}{2}+2kπ$,k∈Z,得$\frac{5}{6}π-2kπ$≤x≤$\frac{π}{6}+2kπ$,k∈Z.
∴函数f(x)的单调递增区间为[$-\frac{5π}{6}+2kπ\;,\;\;\frac{π}{6}+2kπ$],k∈Z;
(2)由已知,有$sin(x-\frac{π}{12}+\frac{π}{3})=sin(x+\frac{π}{4})=-\frac{\sqrt{10}}{5}cos2x$,
于是 $sinxcos\frac{π}{4}+cosxsin\frac{π}{4}=-\frac{{\sqrt{10}}}{5}({cos^2}x-{sin^2}x)$,
即$-\frac{{\sqrt{5}}}{2}(sinx+cosx)=(cosx+sinx)(cosx-sinx)$.
当sinx+cosx=0时,由x是第二象限角,知$x=2kπ+\frac{3π}{4}$,k∈Z.
此时cosx-sinx=$-\frac{{\sqrt{2}}}{2}-\frac{{\sqrt{2}}}{2}=-\sqrt{2}$.
当sinx+cosx≠0时,得$cosx-sinx=-\frac{{\sqrt{5}}}{2}$.
综上所述,$cosx-sinx=-\sqrt{2}$或$-\frac{{\sqrt{5}}}{2}$.
点评 本题考查了三角函数的化简求值,考查了三角函数的周期及单调性,是中档题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
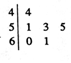 为了检查某高三毕业班学生的体重情况,从该班随机抽取了6位学生进行称重,如图为6位学生体重的茎叶图(单位:kg),其中图中左边是体重的十位数字,右边是个位数字,则这6位学生体重的平均数为( )
为了检查某高三毕业班学生的体重情况,从该班随机抽取了6位学生进行称重,如图为6位学生体重的茎叶图(单位:kg),其中图中左边是体重的十位数字,右边是个位数字,则这6位学生体重的平均数为( )| A. | 52 | B. | 53 | C. | 54 | D. | 55 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x,g(x)=${(\sqrt{x}\;)^2}$ | B. | f(x)=x+1,g(x)=$\frac{{{x^2}-1}}{x-1}$ | ||
| C. | f(x)=|x|,g(x)=$\sqrt{{x}^{2}}$ | D. | f(x)=log22x,g(x)=2log2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | m | C. | 2m | D. | 2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | $({\frac{3}{4},+∞})$ | C. | (0,2) | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com