
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为边长为
为边长为![]() 的正方形,
的正方形,![]() .
.
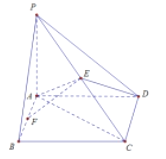
(1)求证:![]() ;
;
(2)若![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题本题主要考查线面垂直的判定与性质、锥体的体积等基础知识,考查学生的分析问题解决问题的能力、空间想象能力、逻辑推理能力、计算能力.第一问,利用线面垂直的判定定理,先证出![]() 平面
平面![]() ,利用线面垂直的性质定理得
,利用线面垂直的性质定理得![]() ,在
,在![]() 中再证明
中再证明![]() ;第二问, 用体积转化法,将
;第二问, 用体积转化法,将![]() 转化为
转化为![]() ,证明出
,证明出![]() 是锥体的高,再利用锥体的个数求解.
是锥体的高,再利用锥体的个数求解.
试题解析:(Ⅰ)连接![]() 交
交![]() 于点
于点![]() ,
,
因为底面![]() 是正方形,
是正方形,
所以![]() 且
且![]() 为
为![]() 的中点.
的中点.
又![]()
所以![]() 平面
平面![]() ,
,
由于![]() 平面
平面![]() ,故
,故![]()
![]() .
.
又![]() ,故
,故![]() .
.
(Ⅱ)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() ∥=
∥=![]() ,
,
所以![]() 为平行四边形,
为平行四边形,![]() ∥
∥![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() 的中点为
的中点为![]() ,
,
所以![]() .
.
由![]() 平面
平面![]() ,又可得
,又可得![]() ,
,
又![]() ,又
,又![]()
所以![]() 平面
平面![]()
所以![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]()
(注意:没有证明出![]() 平面
平面![]() ,直接运用这一结论的,后续过程不给分)
,直接运用这一结论的,后续过程不给分)
![]()
![]()
![]()
故三棱锥D-ACE的体积为![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
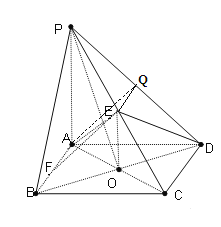
【题目】已知四棱锥![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在底面
在底面![]() 上的射影是
上的射影是![]() 的中点
的中点![]() ,
,![]() .
.
(1)求证:直线![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)当四棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1到9的九个数字中取三个偶数四个奇数,试问:
(1)能组成多少个没有重复数字的七位数?
(2)在(1)中的七位数中三个偶数排在一起的有几个?
(3)在(1)中的七位数中,偶数排在一起、奇数也排在一起的有几个?
(4)在(1)中任意两偶然都不相邻的七位数有几个?
(答题要求:先列式,后计算 , 结果用具体数字表示.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( )
A. 这种抽样方法是一种分层抽样
B. 这种抽样方法是一种系统抽样
C. 这五名男生成绩的方差大于这五名女生成绩的方差
D. 该班级男生成绩的平均数小于该班女生成绩的平均数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,左顶点为
轴上,左顶点为![]() ,左焦点为
,左焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)以![]() 为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,过
,过![]() 点作
点作![]() 的垂线,交
的垂线,交![]() 的延长线于点
的延长线于点![]() ,
,![]() .连结
.连结![]() ,交
,交![]() 于点
于点![]() ,如图1,将
,如图1,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
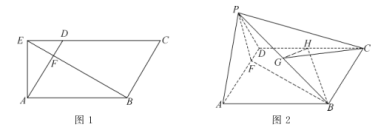
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,且平面
的中点,且平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com