
【题目】已知由自然数组成的![]() 元集合
元集合![]() ,非空集合
,非空集合![]() ,且对任意的
,且对任意的![]() ,都有
,都有![]() .
.
(1)当![]() 时,求所有满足条件的集合
时,求所有满足条件的集合![]() ;
;
(2)当![]() 时,求所有满足条件的集合
时,求所有满足条件的集合![]() 的元素总和;
的元素总和;
(3)定义一个集合的“交替和”如下:按照递减的次序重新排列该集合的元素,然后从最大数开始交替地减、加后继的数.例如集合![]() 的交替和是
的交替和是![]() ,集合
,集合![]() 的交替和为
的交替和为![]() .当
.当![]() 时,求所有满足条件的集合
时,求所有满足条件的集合![]() 的“交替和”的总和.
的“交替和”的总和.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)确定![]() 后可知
后可知![]() 有偶数个元素,分别讨论两个元素和四个元素的情况即可得到结果;
有偶数个元素,分别讨论两个元素和四个元素的情况即可得到结果;
(2)确定![]() 可知
可知![]() 有偶数个元素,分别在两个、四个、六个和八个元素的情况下求解元素之和,加和得到结果;
有偶数个元素,分别在两个、四个、六个和八个元素的情况下求解元素之和,加和得到结果;
(3)由![]() 、
、![]() 和
和![]() 时交替和总和的规律可得到当
时交替和总和的规律可得到当![]() 时,交替和总和为
时,交替和总和为![]() ,代入
,代入![]() 即可求得结果.
即可求得结果.
(1)当![]() 时,
时,![]()
![]() 是
是![]() 的非空子集,且
的非空子集,且![]() 时,
时,![]()
![]()
![]() 中有偶数个元素
中有偶数个元素
![]() 中有两个元素时,
中有两个元素时,![]() 或
或![]()
![]() 中有四个元素时,
中有四个元素时,![]()
![]() 所有满足条件的集合
所有满足条件的集合![]() 有:
有:![]() ,
,![]() ,
,![]()
(2)当![]() 时,
时,![]()
![]() 是
是![]() 的非空子集,且
的非空子集,且![]() 时,
时,![]()
![]()
![]() 中有偶数个元素
中有偶数个元素
当![]() 中有两个元素时,元素之和为:
中有两个元素时,元素之和为:![]()
当![]() 中有四个元素时,元素之和为:
中有四个元素时,元素之和为:![]()
当![]() 中有六个元素时,元素之和为:
中有六个元素时,元素之和为:![]()
当![]() 中有八个元素时,元素之和为:
中有八个元素时,元素之和为:![]()
![]() 所有满足条件的集合
所有满足条件的集合![]() 的元素总和为:
的元素总和为:![]()
(3)当![]() ,
,![]() ,交替和的总和为:
,交替和的总和为:![]()
当![]() 时,由(1)知,交替和的总和为:
时,由(1)知,交替和的总和为:![]()
当![]() 时,
时,![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() ,交替和的总和为:
,交替和的总和为:![]()
……以此类推,当![]() 时,交替和的总和为:
时,交替和的总和为:![]()
当![]() 时,
时,![]()
![]() 所求交替和的总和为:
所求交替和的总和为:![]()


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为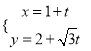 (
(![]() 为参数)
为参数)
写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 经过伸缩变换
经过伸缩变换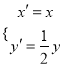 后得到曲线
后得到曲线![]() ,设
,设![]() 为
为![]() 上任意一点,
上任意一点,
求![]() 的最小值,并求相应的点
的最小值,并求相应的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 中点(如图1).将
中点(如图1).将![]() 沿
沿![]() 折起到图2中
折起到图2中![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() .
.

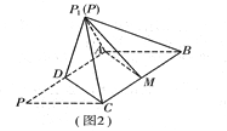
(1)将![]() 沿
沿![]() 折起的过程中,
折起的过程中, ![]() 平面
平面![]() 是否成立?并证明你的结论;
是否成立?并证明你的结论;
(2)若![]() ,过
,过![]() 的平面交
的平面交![]() 于点
于点![]() ,且
,且![]() 为
为![]() 的中点,求三棱锥
的中点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分) 已知双曲线![]() 的两个焦点为
的两个焦点为![]() 的曲线C上.
的曲线C上.
(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q(0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为![]() 求直线l的方程
求直线l的方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的内接等边三角形
的内接等边三角形![]() 的面积为
的面积为![]() (其中
(其中![]() 为坐标原点).
为坐标原点).
(1)试求抛物线![]() 的方程;
的方程;
(2)已知点![]() 两点在抛物线
两点在抛物线![]() 上,
上,![]() 是以点
是以点![]() 为直角顶点的直角三角形.
为直角顶点的直角三角形.
①求证:直线![]() 恒过定点;
恒过定点;
②过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 于点
于点![]() ,试求点
,试求点![]() 的轨迹方程,并说明其轨迹是何种曲线.
的轨迹方程,并说明其轨迹是何种曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨、硝酸盐18吨;生产1车皮乙种肥料的主要原料是磷酸盐1吨、硝酸盐15吨,现库存磷酸盐10吨、硝酸盐66吨,在此基础上生产这两种混合肥料。如果生产1车皮甲种肥料,产生的利润为12000元;生产1车皮乙种肥料,产生的利润为7000元。那么可产生最大的利润是__________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=![]() ,|AF2|=
,|AF2|=![]() .
.
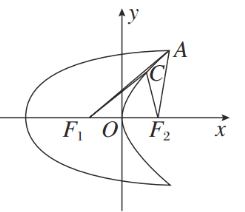
(1)求曲线C1和C2的方程;
(2)设点C是C2上一点,若|CF1|=![]() |CF2|,求△CF1F2的面积.
|CF2|,求△CF1F2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的方程为
的方程为![]() (
(![]() ),点
),点![]() 为坐标原点,点
为坐标原点,点![]() ,
, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() ,点
,点![]() 在线段
在线段![]() 上,满足
上,满足![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,交
两点,交![]() 轴于点
轴于点![]() (
(![]() ),问是否存在实数
),问是否存在实数![]() 使得以
使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求
?若存在,求![]() 的值,若不存在,说出理由.
的值,若不存在,说出理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com