
����Ŀ����2017���ϳ�ɳ��ģ��ij�ֲ�Ʒ��������������ָ��ֵ����������������ָ��ֵ���ֵȼ����±���
����ָ��ֵ |
|
|
|
�ȼ� | ����Ʒ | ����Ʒ | һ��Ʒ |
��ij��ҵ���������ֲ�Ʒ�г�ȡ200��������õ����µ�Ƶ�ʷֲ�ֱ��ͼ��
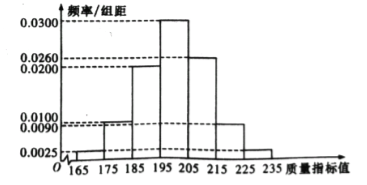
��1���������ϳ����������ݣ��ܷ���Ϊ����ҵ���������ֲ�Ʒ���ϡ�һ������Ʒ����Ҫռȫ����Ʒ90%���Ĺ涨��
��2���������У�����Ʒ�ȼ��÷ֲ�����ķ�����ȡ8�����ٴ���8����Ʒ�������ȡ4�������ȡ��4����Ʒ�У�һ����������Ʒ���еĸ��ʣ�
��3������ҵΪ��߲�Ʒ��������չ�ˡ����������¡��������ٳ�����⣬��Ʒ����ָ��ֵ![]() ��������
��������![]() �������������¡���������ָ��ֵ�ľ�ֵ�Ȼǰ��Լ�����˶��٣�
�������������¡���������ָ��ֵ�ľ�ֵ�Ȼǰ��Լ�����˶��٣�
���𰸡���1��������;��2��![]() ;��3��17.6
;��3��17.6
�������������������1������Ƶ�ʷֲ�ֱ��ͼ��һ������Ʒ��ռ�����Ĺ���ֵΪ
![]() ���������ж�.
���������ж�.
��2����Ƶ�ʷֲ�ֱ��ͼ��Ƶ�ʷֲ���֪8����Ʒ�У�һ��Ʒ3��������Ʒ4��������Ʒ1�����������۸�������ɵ�![]() .
.
��3����������������¡��ǰ�����Ʒ����ָ��ֵΪ![]() ���ɵ�����ָ��ֵ�ľ�ֵ�Ȼǰ��Լ������17.6
���ɵ�����ָ��ֵ�ľ�ֵ�Ȼǰ��Լ������17.6
�����������1�����ݳ����������ݣ�һ������Ʒ��ռ�����Ĺ���ֵΪ![]() �����ڸù���ֵС��0.92���ʲ�����Ϊ����ҵ���������ֲ�Ʒ���ϡ�һ������Ʒ����Ҫռȫ����Ʒ92%���Ĺ涨.
�����ڸù���ֵС��0.92���ʲ�����Ϊ����ҵ���������ֲ�Ʒ���ϡ�һ������Ʒ����Ҫռȫ����Ʒ92%���Ĺ涨.
��2����Ƶ�ʷֲ�ֱ��ͼ֪��һ����������Ʒ��Ƶ�ʷֱ�Ϊ0.375��0.5��0.125�������������÷ֲ����������ȡ��8����Ʒ�У�һ��Ʒ3��������Ʒ4��������Ʒ1�����ٴ���8����Ʒ�������ȡ4����һ����������Ʒ���е������2�֣���һ��Ʒ2��������Ʒ1��������Ʒ1������һ��Ʒ1��������Ʒ2��������Ʒ1����������ĸ���![]() .
.
��3�������������¡��ǰ������ҵ���ֲ�Ʒ������ָ��ֵ�ľ�ֵԼΪ
![]()
![]()
�����������¡����Ʒ����ָ��ֵ![]() ��������
��������![]() ����
����![]() .
.
���ԣ������������¡���������ָ��ֵ�ľ�ֵ�Ȼǰ��Լ������17.6


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ѧ���ϣ���ͻȻ���ѣ����ֺڰ������������ݣ�
������x3��3x��x��[0��+�ޣ�����Сֵ���⣺���û�������ʽa+b+c��3 ![]() ���õ�x3+1+1��3x������x3��3x=x3+1+1��3x��2��3x��3x��2=��2�����ҽ���x=1ʱ��ȡ����Сֵ��2
���õ�x3+1+1��3x������x3��3x=x3+1+1��3x��2��3x��3x��2=��2�����ҽ���x=1ʱ��ȡ����Сֵ��2
��1����ʦ����ģ�����⣬�о�x4��4x��x��[0��+�ޣ��ϵ���Сֵ��
����ʾ��a+b+c+d��4 ![]() ��
��
��2���о� ![]() x3��3x��x��[0��+�ޣ��ϵ���Сֵ��
x3��3x��x��[0��+�ޣ��ϵ���Сֵ��
��3�������a��0ʱ��x3��ax��x��[0��+�ޣ�����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017��������ɽ��ģ����֪��Բ������![]() ������
������![]() ���Ͻصõ��ҳ�Ϊ4���Ƕ�ԲԲ�ĵĹ켣Ϊ����C��
���Ͻصõ��ҳ�Ϊ4���Ƕ�ԲԲ�ĵĹ켣Ϊ����C��
������ֱ��![]() ������CΧ�ɵ����������
������CΧ�ɵ����������
����![]() ��ֱ��
��ֱ��![]() �ϣ���
�ϣ���![]() ������
������![]() ������C������
������C������![]() ��
��![]() ���е�ֱ�Ϊ
���е�ֱ�Ϊ![]() ��
��![]() ��֤�������ڳ���
��֤�������ڳ���![]() ��ʹ��
��ʹ��![]() ������
������![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x���Ƕ�����R�ϵ�ż��������������[0��+�ޣ��ϵ����ݼ�����f��log2a��+f��2log ![]() a����2f����1������ʵ��a��ȡֵ��Χ�� ��
a����2f����1������ʵ��a��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У��١���m��0����x2��x+m=0��ʵ���� �ڡ���x��1��y��1����x+y��2�������⣮ �ۡ��������x��{x|��2��x��4}��|x��2|��3�ķ���ʽ�� �ܡ�����0��һԪ���η���ax2+bx+c=0��һ������һ�����ij�Ҫ����������������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������f��x��= ![]() ���溯������ʹf��x����3������x��ȡֵ��ΧΪ�� ��
���溯������ʹf��x����3������x��ȡֵ��ΧΪ�� ��
A.�����ޣ���1��
B.����1��0��
C.��0��1��
D.��1��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}��ǰn���ΪSn �� �����������������n����Sn=2an��3n��
��1����bn=an+3����֤������{bn}�ǵȱ����У������{an}��ͨ�ʽ��
��2��������{nan}��ǰn��ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij�β����У���6λͬѧ��ƽ���ɼ�Ϊ75�֣���xn��ʾ���Ϊn��n=1��2������6����ͬѧ���óɼ�����ǰ5λͬѧ�ijɼ����£�
���n | 1 | 2 | 3 | 4 | 5 |
�ɼ�xn | 70 | 76 | 72 | 70 | 72 |
��1�����6λͬѧ�ijɼ�x6 �� ����6λͬѧ�ɼ��ı���s��
��2����ǰ5λͬѧ�У������ѡ2λͬѧ����ǡ��1λͬѧ�ɼ������䣨68��75���еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ѧ��������״����ijУ�����ȡ��һ��ѧ���������أ���ͳ�ƣ�����ѧ�����������ݣ���λ��ǧ�ˣ�ȫ������45��70֮�䣮�����ݷֳ�����5�飺��1��[45��50������2��[50��55������3��[55��60������4��[60��65������5��[65��70]���õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ���ֲ��÷ֲ�����ķ������ӵ�3��4��5���������ȡ6��ѧ�������죮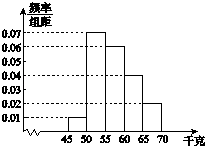
��1����ÿ���ȡ��ѧ��������
��2������6��ѧ�����ٴ������ȡ2��ѧ�����и��죬����2��ѧ������ͬһ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com