
分析 (1)利用相互独立事件的概率计算公式即可得出.
(2)记女生四关都闯过为事件B,则$P(B)=\frac{4}{5}×\frac{3}{4}×\frac{2}{3}×\frac{1}{2}=\frac{1}{5}$,?的取值可能为0,1,2,3,4,利用相互独立与互斥事件的概率计算公式即可得出.
解答 解:(1)记男生四关都闯过为事件A,则$P(A)=\frac{5}{6}×\frac{4}{5}×\frac{3}{4}×\frac{2}{3}=\frac{1}{3}$.
(2)记女生四关都闯过为事件B,则$P(B)=\frac{4}{5}×\frac{3}{4}×\frac{2}{3}×\frac{1}{2}=\frac{1}{5}$,
因为$P({ε=0})={({\frac{2}{3}})^2}{({\frac{4}{5}})^2}=\frac{64}{225}$,$P({ε=1})=C_2^1\frac{1}{3}•\frac{2}{3}{({\frac{4}{5}})^2}+C_2^1\frac{1}{5}•\frac{4}{5}•{({\frac{2}{3}})^2}=\frac{96}{225}$,$P({ε=2})=C_2^2{({\frac{1}{3}})^2}{({\frac{4}{5}})^2}+C_2^2{({\frac{1}{5}})^2}{({\frac{2}{3}})^2}+C_2^1\frac{1}{3}•\frac{2}{3}•C_2^1•\frac{1}{5}•\frac{4}{5}=\frac{52}{225}$,$P({ε=3})=C_2^1\frac{1}{3}•\frac{2}{3}{({\frac{1}{5}})^2}+C_2^1\frac{1}{5}•\frac{4}{5}•{({\frac{1}{3}})^2}=\frac{12}{225}$,$P({ε=4})={({\frac{1}{3}})^2}{({\frac{1}{5}})^2}=\frac{1}{225}$.
所以的分布列如下:
| ? | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{64}{225}$ | $\frac{96}{225}$ | $\frac{52}{225}$ | $\frac{12}{225}$ | $\frac{1}{225}$ |
点评 本题考查了相互独立与互斥事件的概率计算公式、随机变量的分布列与数学期望计算公式,考查了推理能力与计算能力,属于中档题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:高中数学 来源: 题型:解答题
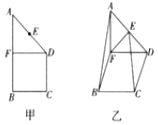 如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.
如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P | B. | Q | C. | {-1,1} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在一次抽样调查中测得样本的5个样本点,数值如表:
在一次抽样调查中测得样本的5个样本点,数值如表:| x | 0.25 | 0.5 | 1 | 2 | 4 |
| y | 16 | 12 | 5 | 2 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的图象关于直线x=$\frac{π}{3}$对称 | |
| B. | f(x)的图象关于点($\frac{π}{4}$,0)对称 | |
| C. | 把f(x)的图象向左平移$\frac{π}{12}$个单位长度,得到一个偶函数的图象 | |
| D. | f(x)的最小正周期为π,且在[0,$\frac{π}{6}$]上为增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com