
在△ABC中,a、b、c分别是角A、B、C的对边,且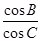 =-
=-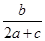 .
.
(2)若b= ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.
(1) (2)
(2)
解析试题分析:(1)利用正弦定理化简已知的等式,移项后再利用两角和与差的正弦函数公式及诱导公式化简,根据sinA不为0,得出cosB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数;
(2)由第一问求出的B的度数,得出cosB的值,利用余弦定理表示出b2,把b及cosB的值代入,配方后再把a+c的值代入可得出ac=6,与a+c=5联立成方程组,求出方程组的解即可求出a与c的值。根据正弦定理可知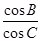 =-
=-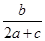 .,得到-sinBcosC=2cosBsinA+cosBsinC(3分)sinBcosC+cosBsinC+2cosBsinA=0,
.,得到-sinBcosC=2cosBsinA+cosBsinC(3分)sinBcosC+cosBsinC+2cosBsinA=0,
sin(B+C)+2cosBsinA=0,(4分)sinA+2cosBsinA=0,(只要写出本行,给5分)(5分)因为sinA≠0,所以cosB=-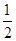 ,所以B=120°;(7分)(2)由余弦定理得:b2=a2+c2-2accosB,(9分)19=(a+c)2-2ac-2accos120°,所以ac=6,(11分)由a+c=5,ac=6,可得a=2,c=3,或a=3,c=2.,故可知
,所以B=120°;(7分)(2)由余弦定理得:b2=a2+c2-2accosB,(9分)19=(a+c)2-2ac-2accos120°,所以ac=6,(11分)由a+c=5,ac=6,可得a=2,c=3,或a=3,c=2.,故可知 ,
,
考点:正弦、余弦定理
点评:此题考查了正弦、余弦定理,两角和与差的正弦函数公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.


科目:高中数学 来源: 题型:解答题
位于A处的雷达观测站,发现其北偏东45°,与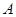 相距20
相距20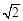 海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东
海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东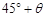
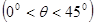 的C处,
的C处,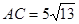 .在离观测站A的正南方某处E,
.在离观测站A的正南方某处E,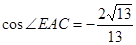
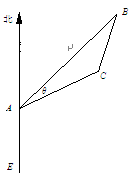
(1)求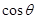 ; (2)求该船的行驶速度v(海里/小时);
; (2)求该船的行驶速度v(海里/小时);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com