
【题目】设函数![]() 的单调减区间是
的单调减区间是![]() 。
。
(1)求![]() 的解析式;
的解析式;
(2)若对任意的![]() ,关于
,关于![]() 的不等式
的不等式![]() 在
在
![]() 时有解,求实数
时有解,求实数![]() 的取值范围。
的取值范围。
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)f'(x)=3ax2+2bx+c.由f(x)的单调减区间是(1,2),知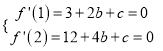 ,由此能求出f(x)的解析式.
,由此能求出f(x)的解析式.
(2)由(1)得f'(x)=3x2﹣9x+6=3(x﹣1)(x﹣2),当x∈[2,+∞)时,f'(x)≥0,故f(x)在[2,+∞)单调递增,所以f(x)min=f(2)=3.要使关于x的不等式![]() 在x∈[2,+∞)时有解,只需
在x∈[2,+∞)时有解,只需![]() 在m∈(0,2]恒成立.由此能求出实数t的取值范围.
在m∈(0,2]恒成立.由此能求出实数t的取值范围.
试题解析:
⑴![]() .
.
∵![]() 的单调减区间是(1,2),∴
的单调减区间是(1,2),∴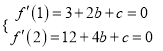 ,
,
∴![]() ∴
∴![]() .
.
⑵由⑴得![]() ,
,
当![]() 时,
时, ![]() ≥0,∴
≥0,∴![]() 在
在![]() 单调递增,∴
单调递增,∴![]()
![]() .
.
要使关于![]() 的不等式
的不等式![]() 在
在![]() 时有解,
时有解,
即![]() ,即
,即![]() 对任意
对任意![]() 恒成立,
恒成立,
只需![]() 在
在![]() 恒成立.
恒成立.
设![]() ,
, ![]() ,则
,则![]() 。
。![]() ,
,
当![]() 时,
时, ![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
∴![]() .
.![]()


科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2-x+m,且f(log2a)=m,log2f(a)=2,(a≠1).
(1)求a,m的值;
(2)求f(log2x)的最小值及对应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】片森林原来面积为a,计划每年砍伐森林面积是上一年末森林面积的p%,当砍伐到原来面积的一半时,所用时间是10年,已知到今年末为止,森林剩余面积为原来面积的![]() ,为保护生态环境,森林面积至少要保留原来面积的
,为保护生态环境,森林面积至少要保留原来面积的![]() .
.
(1)求每年砍伐面积的百分比p%;
(2)到今年为止,该森林已砍伐了多少年?
(3)今年以后至多还能再砍伐多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:
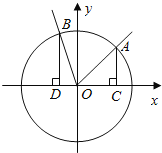
【题目】如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且![]() .将角α的终边按逆时针方向旋转
.将角α的终边按逆时针方向旋转![]() ,交单位圆于点B.记A(x1,y1),B(x2,y2).
,交单位圆于点B.记A(x1,y1),B(x2,y2).
(Ⅰ)若![]() ,求x2;
,求x2;
(Ⅱ)分别过A,B作x轴的垂线,垂足依次为C,D.记△AOC的面积为S1,△BOD的面积为S2.若S1=2S2,求角α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.

(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)求证:AC∥平面DEF;
(Ⅲ)求三棱锥A—DEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把下列演绎推理写成三段论的形式.
(1)在标准大气压下,水的沸点是100℃,所以在标准大气压下把水加热到100℃时,水会沸腾;
(2)一切奇数都不能被2整除, ![]() 是奇数,所以
是奇数,所以![]() 不能被2整除;
不能被2整除;
(3)三角函数都是周期函数, ![]() 是三角函数,因此
是三角函数,因此![]() 是周期函数.
是周期函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=xa的图象过点(2,4).
(1)求函数f(x)的解析式;
(2)设函数h(x)=4f(x)-kx-8在[5,8]上是单调函数,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com