
|
|
| AC |
| BD |
| PA |
| PD |
| AC |
| BD |
| PA |
| PD |
| PA•PB |
| 45×(45+35) |
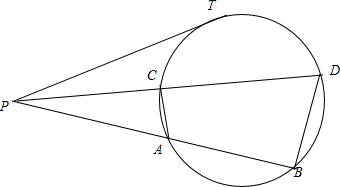
| OA2+OB2-2OA•OBcos∠AOB |
|
|
|


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案科目:高中数学 来源:2014届湖北省高二9月调研考试理科数学试卷(解析版) 题型:解答题
(本小题满分14分)某城市自西向东和自南向北的两条主干道的东南方位有一块空地市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,

其中, 分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点
分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点 处修一条步行小道,小道为抛物线
处修一条步行小道,小道为抛物线 的一段,在小道上依次以点
的一段,在小道上依次以点
 为圆心,修一系列圆型小道,这些圆型小道与主干道
为圆心,修一系列圆型小道,这些圆型小道与主干道 相切,且任意相邻的两圆彼此外切,若
相切,且任意相邻的两圆彼此外切,若 (单位:百米)且
(单位:百米)且 .
.
(1)记以 为圆心的圆与主干道
为圆心的圆与主干道 切于
切于 点,证明:数列
点,证明:数列 是等差数列,并求
是等差数列,并求 关于
关于 的表达式;
的表达式;
(2)记 的面积为
的面积为 ,根据以往施工经验可知,面积为
,根据以往施工经验可知,面积为 的圆型小道的施工工时为
的圆型小道的施工工时为 (单位:周).试问5周时间内能否完成前
(单位:周).试问5周时间内能否完成前 个圆型小道的修建?请说明你的理由.
个圆型小道的修建?请说明你的理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三下学期模拟冲刺考试理科数学试卷(解析版) 题型:解答题
(本小题满分l2分)某市第一中学要用鲜花布置花圃中 五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
(1)当 区域同时用红色鲜花时,求布置花圃的不同方法的种数;
区域同时用红色鲜花时,求布置花圃的不同方法的种数;
(2)求恰有两个区域用红色鲜花的概率;
(3)记 为花圃中用红色鲜花布置的区域的个数,求随机变量
为花圃中用红色鲜花布置的区域的个数,求随机变量 的分布列及其数学期望.
的分布列及其数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2006-2007学年广东省深圳市龙华中英文实验学校高三(上)11月月考数学试卷(文科)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com