练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本小题共12分） 证明函数在上是增函数。

    略

    解析证明：任取，且，则··2分
    ·····9分
    因为，得···········11分
    所以函数在上是增函数····················12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    集合M＝{a，b，c}，N＝{－1,0,1}，映射f：M→N满足f(a)＋f(b)＋f(c)＝0，那么映射f：M→N的个数是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题满分10分）
    求下列函数的定义域  

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题8分）经过调查发现，某种新产品在投放市场的30天中,前20天其价格直线上升，后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示：

    时间
    		第4天
    		第12天
    		第20天
    		第28天
    价格
    (千元)
    		34
    		42
    		50
    		34
     
    （1）写出价格关于时间的函数表达式（表示投放市场的第天）
    （2）若销售量与时间的函数关系式为：，问该产品投放市场第几天，日销售额最高?

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设二次函数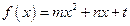的图像过原点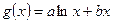，，的导函数为，且，
    （1）求函数，的解析式；
    （2）求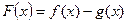的极小值；
    （3）是否存在实常数和，使得和若存在，求出和的值；若不存在，说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本大题满分13分)
    已知函数在处取得极值
    （1）求b与a的关系；
    （2）设函数，如果在区间(0,1)上存在极小值，求实数a的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题满分14分）
    把下列各式分解因式
    （1）         （2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分10分）
    小刘家要建造一个长方形无盖蓄水池，其容积为48，深为3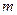.如果池底每平方米的造价为150元，池壁每平方米的造价为120元，怎样设计水池能使总造价最低？最低造价是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数
    （1）求函数的最小值和最小正周期；
    （2）设△的内角对边分别为，且，若与共线，求的值.

    查看答案和解析>>

    同步练习册答案