练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某校田径队共有男运动员45人，女运动员36人．若采用分层抽样的方法在全体运动员中抽取18人进行体质测试，则抽到的女运动员人数为 ．

    【答案】8
    【解析】解：∵某校田径队共有男运动员45人，女运动员36人，

    ∴这支田径队共有45+36=81人，

    用分层抽样的方法从该队的全体运动员中抽取一个容量为18的样本，

    ∴每个个体被抽到的概率是 = ，

    ∵女运动员36人，

    ∴女运动员要抽取36× =8人，

    所以答案是：8．

    【考点精析】利用分层抽样对题目进行判断即可得到答案，需要熟知先将总体中的所有单位按照某种特征或标志（性别、年龄等）划分成若干类型或层次，然后再在各个类型或层次中采用简单随机抽样或系用抽样的办法抽取一个子样本，最后，将这些子样本合起来构成总体的样本．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题： ①﹣3是函数y=f（x）的极值点；
    ②﹣1是函数y=f（x）的最小值点；
    ③y=f（x）在x=0处切线的斜率小于零；
    ④y=f（x）在区间（﹣3，1）上单调递增．
    则正确命题的序号是 ．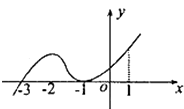

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= 过点（1，e）．
    （1）求y=f（x）的单调区间；
    （2）当x＞0时，求 的最小值；
    （3）试判断方程f（x）﹣mx=0（m∈R且m为常数）的根的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 a,b 为实数,且 a>0,b>0 ,
    （1）求证: ;
    （2）求(5-2a)2+4b2+(a-b)2 的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 m>1 且关于 x 的不等式 的解集为 [0,4] .
    ①求 m 的值；
    ②若 a ， b 均为正实数，且满足 a+b=m ，求 a2+b2 的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 的三个内角 A,B,C 成等差数列，且 a,b,c 分别为角 A,B,C 的对边，求证：(a+b)-1+(b+c)-1=3(a+b+c)-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆E： + =1（a＞b＞0）的右焦点为F，短轴的一个端点为M，直线l：3x﹣4y=0交椭圆E于A，B两点，若|AF|+|BF|=4，点M到直线l的距离不小于 ，则椭圆E的离心率的取值范围是（ ）
    A.（0， ]
    B.（0， ]
    C.[ ，1）
    D.[ ，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝log2(x＋m)，且f(0)、f(2)、f(6)成等差数列.
    （1）求f(30)的值.
    （2）若a、b、c是两两不相等的正数，且a、b、c成等比数列，试判断f(a)＋f(c)与2f(b)的大小关系，并证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2015年下学期某市教育局对某校高三文科数学进行教学调研，从该校文科生中随机抽取40名学生的数学成绩进行统计，将他们的成绩分成六段[80，90），[90，100），[100，110），[110，120），[120，130），[130，140）后得到如图所示的频率分布直方图．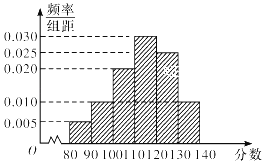

    （1）求这40名学生中数学成绩不低于120分的学生人数；
    （2）若从数学成绩[80，100）内的学生中任意抽取2人，求成绩在[80，90）中至少有一人的概率．

    查看答案和解析>>

    同步练习册答案