
【题目】如图,在菱形 ![]() 中,
中, ![]() ⊥平面
⊥平面 ![]() ,且四边形
,且四边形 ![]() 是平行四边形.
是平行四边形.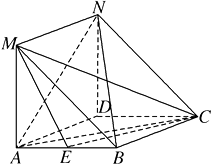
(1)求证: ![]() ;
;
(2)当点 ![]() 在
在 ![]() 的什么位置时,使得
的什么位置时,使得 ![]() ∥平面
∥平面 ![]() ,并加以证明.
,并加以证明.
【答案】
(1)证明:连接BD , 则AC⊥BD.
由已知得DN⊥平面ABCD , 因为AC平面ABCD , 所以DN⊥AC.
因为DN平面NDB , BD平面NDB , DN∩DB=D ,
所以AC⊥平面NDB.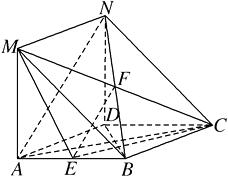
又BN平面NDB ,
所以AC⊥BN.
(2)解:当E为AB的中点时,有AN∥平面MEC.
设CM与BN交于F , 连接EF.
由已知可得四边形BCNM是平行四边形,F是BN的中点,
因为E是AB的中点,
所以AN∥EF.
又EF平面MEC , AN平面MEC ,
所以AN∥平面MEC.
【解析】(1)要证明AC⊥BN,只要证明AC⊥平面NDB,而由已知可知AC⊥BD,则只要证出AC⊥DN,结合已知容易证明
(2)当E为AB的中点时,设CM与BN交于F,由已知可得AN∥EF,结合线面平行的判定定理可证.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】P(x0 , y0)(x0≠±a)是双曲线E: ![]() 上一点,M,N分别是双曲线E的左右顶点,直线PM,PN的斜率之积为
上一点,M,N分别是双曲线E的左右顶点,直线PM,PN的斜率之积为 ![]() .
.
(1)求双曲线的离心率;
(2)过双曲线E的右焦点且斜率为1的直线交双曲线于A,B两点,O为坐标原点,C为双曲线上一点,满足 ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 在椭圆C:
在椭圆C: ![]() 上,F为右焦点,PF⊥垂直于x轴,A,B,C,D为椭圆上的四个动点,且AC,BD交于原点O.
上,F为右焦点,PF⊥垂直于x轴,A,B,C,D为椭圆上的四个动点,且AC,BD交于原点O.
(1)求椭圆C的方程;
(2)判断直线l: ![]() 与椭圆的位置关系;
与椭圆的位置关系;
(3)设A(x1 , y1),B(x2 , y2)满足 ![]() =
= ![]() ,判断kAB+kBC的值是否为定值,若是,请求出此定值,并求出四边形ABCD面积的最大值,否则说明理由.
,判断kAB+kBC的值是否为定值,若是,请求出此定值,并求出四边形ABCD面积的最大值,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校10位同学组成的志愿者组织分别由李老师和杨老师负责.每次献爱心活动均需该组织4位同学参加.假设李老师和杨老师分别将各自活动通知的信息独立、随机地发给4位同学,且所发信息都能收到.则甲同学收到李老师或杨老师所发活动通知信息的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一张坐标纸上涂着圆E: ![]() 及点P(1,0),折叠此纸片,使P与圆周上某点P'重合,每次折叠都会留下折痕,设折痕与直线EP'交于点M .
及点P(1,0),折叠此纸片,使P与圆周上某点P'重合,每次折叠都会留下折痕,设折痕与直线EP'交于点M .
(1)求 ![]() 的轨迹
的轨迹 ![]() 的方程;
的方程;
(2)直线 ![]() 与C的两个不同交点为A , B , 且l与以EP为直径的圆相切,若
与C的两个不同交点为A , B , 且l与以EP为直径的圆相切,若 ![]() ,求△ABO的面积的取值范围.
,求△ABO的面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com