
【题目】函数![]() 满足如下四个条件:
满足如下四个条件:
①定义域为![]() ;
;
②![]() ;
;
③当![]() 时,
时,![]() ;
;
④对任意![]() 满足
满足![]() .
.
根据上述条件,求解下列问题:
⑴求![]() 及
及![]() 的值.
的值.
⑵应用函数单调性的定义判断并证明![]() 的单调性.
的单调性.
⑶求不等式![]() 的解集.
的解集.
 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】《中国诗词大会》节目组决定把《将进酒》、《山居秋暝》、《望岳》、《送杜少府之任蜀州》和另外确定的两首诗词排在后六场,并要求《将进酒》与《望岳》相邻,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻,且均不排在最后,则后六场开场诗词的排法有_____________种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数F(x)=min{2|x1|,x22ax+4a2},
,函数F(x)=min{2|x1|,x22ax+4a2},
其中min{p,q}=![]()
(Ⅰ)求使得等式F(x)=x22ax+4a2成立的x的取值范围;
(Ⅱ)(ⅰ)求F(x)的最小值m(a);
(ⅱ)求F(x)在区间[0,6]上的最大值M(a).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,椭圆C:![]() 的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,若|OB|,|OF2|,|AB|成等比数列,椭圆C上的点到焦点F2的最短距离为
的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,若|OB|,|OF2|,|AB|成等比数列,椭圆C上的点到焦点F2的最短距离为![]() .
.
(1)求椭圆C的标准方程;
(2)设T为直线x=-3上任意一点,过F1的直线交椭圆C于点P,Q,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于两条平行直线![]() 、
、![]() (
(![]() 在
在![]() 下方)和图象
下方)和图象![]() 有如下操作:将图象
有如下操作:将图象![]() 在直线
在直线![]() 下方的部分沿直线
下方的部分沿直线![]() 翻折,其余部分保持不变,得到图象
翻折,其余部分保持不变,得到图象![]() ;将图象
;将图象![]() 在直线
在直线![]() 上方的部分沿直线
上方的部分沿直线![]() 翻折,其余部分保持不变,得到图象
翻折,其余部分保持不变,得到图象![]() :再将图
:再将图![]() 在直线下方的部分沿直线
在直线下方的部分沿直线![]() 翻折,其余部分保持不变,得到图象
翻折,其余部分保持不变,得到图象![]() ;再将图象
;再将图象![]() 在直线
在直线![]() 上方的部分沿直线
上方的部分沿直线![]() 翻折,其余部分保持不变,得到图象
翻折,其余部分保持不变,得到图象![]() ;以此类推…;直到图象
;以此类推…;直到图象![]() 上所有点均在
上所有点均在![]() 、
、![]() 之间(含
之间(含![]() 、
、![]() 上)操作停止,此时称图象
上)操作停止,此时称图象![]() 为图象
为图象![]() 关于直线
关于直线![]() 、
、![]() 的“衍生图形”,线段
的“衍生图形”,线段![]() 关于直线
关于直线![]() 、
、![]() 的“衍生图形”为折线段
的“衍生图形”为折线段![]() .
.
(1)直线型
平面直角坐标系中,设直线![]() ,直线
,直线![]()
①令图象![]() 为
为![]() 的函数图象,则图象
的函数图象,则图象![]() 的解析式为
的解析式为
②令图像![]() 为
为![]() 的函数图象,请你画出
的函数图象,请你画出![]() 和
和![]() 的图象
的图象

③若函数![]() 的图象与图象
的图象与图象![]() 有且仅有一个交点,且交点在
有且仅有一个交点,且交点在![]() 轴的左侧,那么
轴的左侧,那么![]() 的取值范围是_______.
的取值范围是_______.
④请你观察图象![]() 并描述其单调性,直接写出结果_______.
并描述其单调性,直接写出结果_______.
⑤请你观察图象![]() 并判断其奇偶性,直接写出结果_______.
并判断其奇偶性,直接写出结果_______.
⑥图象![]() 所对应函数的零点为_______.
所对应函数的零点为_______.
⑦任取图象![]() 中横坐标
中横坐标![]() 的点,那么在这个变化范围中所能取到的最高点的坐标为(_______,_______),最低点坐标为(_______,_______).
的点,那么在这个变化范围中所能取到的最高点的坐标为(_______,_______),最低点坐标为(_______,_______).
⑧若直线![]() 与图象
与图象![]() 有2个不同的交点,则
有2个不同的交点,则![]() 的取值范围是_______.
的取值范围是_______.
⑨根据函数图象,请你写出图象![]() 的解析式_______.
的解析式_______.
(2)曲线型
若图象![]() 为函数
为函数![]() 的图象,
的图象,
平面直角坐标系中,设直线![]() ,直线
,直线![]() ,
,
则我们可以很容易得到![]() 所对应的解析式为
所对应的解析式为![]() .
.

①请画出![]() 的图象,记
的图象,记![]() 所对应的函数解析式为
所对应的函数解析式为![]() .
.
②函数![]() 的单调增区间为_______,单调减区间为_______.
的单调增区间为_______,单调减区间为_______.
③当![]() 时候,函数
时候,函数![]() 的最大值为_______,最小值为_______.
的最大值为_______,最小值为_______.
④若方程![]() 有四个不同的实数根,则
有四个不同的实数根,则![]() 的取值范围为_______.
的取值范围为_______.
(3)封闭图形型
平面直角坐标系中,设直线![]() ,直线
,直线![]()
设图象![]() 为四边形
为四边形![]() ,其顶点坐标分别为
,其顶点坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 关于直线
关于直线![]() 、
、![]() 的“衍生图形”为
的“衍生图形”为![]() .
.
①![]() 的周长为_______.
的周长为_______.
②若直线![]() 平分
平分![]() 的周长,则
的周长,则![]() _______.
_______.
③将![]() 沿右上方
沿右上方![]() 方向平移
方向平移![]() 个单位,则平移过程中
个单位,则平移过程中![]() 所扫过的面积为_______.
所扫过的面积为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用![]() ,
,![]() 分别表示乌龟和兔子所行的路程,
分别表示乌龟和兔子所行的路程,![]() 为时间,则与故事情节相吻合的是( )
为时间,则与故事情节相吻合的是( )
A.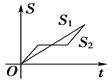 B.
B.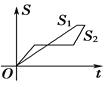 C.
C.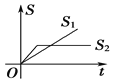 D.
D.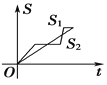
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(1)判断函数f(x)的奇偶性;
(2)判断并用定义证明函数f(x)在其定义域上的单调性.
(3)若对任意的t![]() 1,不等式f(
1,不等式f(![]() )+f(
)+f(![]() )<0恒成立,求k的取值范围.
)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中,椭圆C的参数方程为 ![]() (θ为参数).
(θ为参数).
(1)以原点为极点,x轴的正半轴为极轴建立极坐标系,求椭圆C的极坐标方程;
(2)设M(x,y)为椭圆C上任意一点,求x+2y的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com