
【题目】近年来,随着汽车消费的普及,二手车流通行业得到迅猛发展.某汽车交易市场对2017 年成交的二手车的交易前的使用时间(以下简称“使用时间”)进行统计,得到如图1所示的频率分布直方图,在图1对使用时间的分组中,将使用时间落入各组的频率视为概率.


(1)若在该交易市场随机选取3辆2017年成交的二手车,求恰有2辆使用年限在![]() 的概率;
的概率;
(2)根据该汽车交易市场往年的数据,得到图2所示的散点图,其中![]() (单位:年)表示二手车的使用时间,
(单位:年)表示二手车的使用时间,![]() (单位:万元)表示相应的二手车的平均交易价格.
(单位:万元)表示相应的二手车的平均交易价格.
①由散点图判断,可采用作为该交易市场二手车平均交易价格![]() 关于其使用年限
关于其使用年限![]() 的回归方程,相关数据如下表(表中
的回归方程,相关数据如下表(表中![]() ):
):

试选用表中数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
②该汽车交易市场拟定两个收取佣金的方案供选择.
甲:对每辆二手车统—收取成交价格的![]() 的佣金;
的佣金;
乙:对使用8年以内(含8年)的二手车收取成交价格的![]() 的佣金,对使用时间8年以上(不含 8年)的二手车收取成交价格的
的佣金,对使用时间8年以上(不含 8年)的二手车收取成交价格的![]() 的佣金.
的佣金.
假设采用何种收取佣金的方案不影响该交易市场的成交量,根据回归方程和图表1,并用,各时间组的区间中点值代表该组的各个值.判断该汽车交易市场应选择哪个方案能获得更多佣金.
附注:
于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() ;
;
②参考数据:![]() ,
,![]() .
.
【答案】(1)0.288;(2)①![]() ,②见解析.
,②见解析.
【解析】分析:(1)由频率分布直方图知,在该汽车交易市场2017年成交的二手车随机选取1辆,使用时间在![]() 的概率为
的概率为![]() , 则所求的概率为
, 则所求的概率为![]() .
.
(2)①由题意可得![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,则
,则![]() 关于
关于![]() 的回归方程为
的回归方程为![]() .
.
②根据频率分布直方图和①中的回归方程,对成交的二手汽车可预测:若采用甲方案,预计该汽车交易市场对于成交的每辆车可获得的平均佣金为![]() 万元;若采用乙方案,预计该汽车交易市场对于成交的每辆车可获得的平均佣金为:
万元;若采用乙方案,预计该汽车交易市场对于成交的每辆车可获得的平均佣金为:![]() 万元.则采用甲方案能获得更多佣金.
万元.则采用甲方案能获得更多佣金.
详解:(1)由频率分布直方图知,该汽车交易市场2017年成交的二手车使用时间在![]()
的频率为![]() ,使用时间在
,使用时间在![]() 的频率为
的频率为![]() .
.
所以在该汽车交易市场2017年成交的二手车随机选取1辆,
其使用时间在![]() 的概率为
的概率为![]() ,
,
所以所求的概率为![]() .
.
(2)①由![]() 得
得![]() ,则
,则![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
由于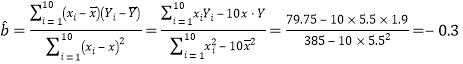
![]() ,
,
则![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,
,
所以![]() 关于
关于![]() 的回归方程为
的回归方程为![]()
②根据频率分布直方图和①中的回归方程,对成交的二手汽车可预测:
使用时间在![]() 的频率为
的频率为![]() ,
,
对应的成交价格的预测值为![]() ;
;
使用时间在![]() 的频率为
的频率为![]() ,
,
对应的成交价格预测值为![]() ;
;
使用时间在![]() 的频率为
的频率为![]() ,
,
对应的成交价格的预测值为![]() ;
;
使用时间在![]() 的频率为
的频率为![]() ,
,
对应的成交价格的预测值为![]() ;
;
使用时间在![]() 的频率为
的频率为![]() ,
,
对应的成交价格的预测值为![]() .
.
若采用甲方案,预计该汽车交易市场对于成交的每辆车可获得的平均佣金为
![]()
=![]() 万元;
万元;
若采用乙方案,预计该汽车交易市场对于成交的每辆车可获得的平均佣金为:
![]()
![]() 万元.
万元.
因为![]() ,所以采用甲方案能获得更多佣金.
,所以采用甲方案能获得更多佣金.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】设数列![]() 的首项
的首项![]() ,前
,前![]() 项和
项和![]() 满足关系式
满足关系式![]() .
.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)设数列![]() 的公比为
的公比为![]() ,作数列
,作数列![]() ,使
,使![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)数列![]() 满足条件(2),求和:
满足条件(2),求和:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核都是“合格”,则该课程考核“合格”,若甲、乙、丙三人在理论考核中合格的概率分别为0.9,0.8,0.7,在实验考核中合格的概率分别为0.8,0.7,0.9,所有考核是否合格相互之间没有影响.
(1)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(2)求这三个人该课程考核都合格的概率(结果保留三位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(请写出式子在写计算结果)有4个不同的小球,4个不同的盒子,现在要把球全部放入盒内:
(1)共有多少种方法?
(2)若每个盒子不空,共有多少种不同的方法?
(3)恰有一个盒子不放球,共有多少种放法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com