
【题目】某种放射性元素的原子数N随时间t的变化规律是N=N0e﹣λt , 其中e=2.71828…为自然对数的底数,N0 , λ是正的常数
(Ⅰ)当N0=e3 , λ=![]() , t=4时,求lnN的值
, t=4时,求lnN的值
(Ⅱ)把t表示原子数N的函数;并求当N=![]() , λ=
, λ=![]() 时,t的值(结果保留整数)
时,t的值(结果保留整数)
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.若sinC+sin(B﹣A)=sin2A,则△ABC的形状为( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣3)2+(y﹣4)2=4. (Ⅰ) 若直线l过点A(2,3)且被圆C截得的弦长为2 ![]() ,求直线l的方程;
,求直线l的方程;
(Ⅱ) 若直线l过点B(1,0)与圆C相交于P,Q两点,求△CPQ的面积的最大值,并求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB. (Ⅰ)证明:A=2B
(Ⅱ)若△ABC的面积S= ![]() ,求角A的大小.
,求角A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某青年教师有一专项课题是进行“学生数学成绩与物理成绩的关系”的研究,他调查了某中学高二年级800名学生上学期期末考试的数学和物理成绩,把成绩按优秀和不优秀分类得到的结果是:数学和物理都优秀的有60人,数学成绩优秀但物理不优秀的有140人,物理成绩优秀但数学不优秀的有60人. 附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 |
k0 | 6.635 | 7.879 | 10.828 |
K2= ![]() .
.
(1)能否在犯错概率不超过0.001的前提下认为该中学学生的数学成绩与物理成绩有关?
(2)将上述调查所得到的频率视为概率,从全体高二年级学生成绩中,有放回地随机抽取4名学生的成绩,记抽取的4份成绩中数学、物理两科成绩恰有一科优秀的份数为X,求X的分布列和期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
回归方程为 ![]() =bx+a,其中b=
=bx+a,其中b= 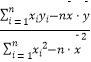 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,求出y与x的回归方程 ![]() =bx+a;
=bx+a;
(3)预测销售额为115万元时,大约需要多少万元广告费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( ) 
A.2,5
B.2,4
C.0,4
D.0,5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C: ![]() =1(0<b<3)的右焦点为F,P为椭圆上一动点,连接PF交椭圆于Q点,且|PQ|的最小值为
=1(0<b<3)的右焦点为F,P为椭圆上一动点,连接PF交椭圆于Q点,且|PQ|的最小值为 ![]() .
. 
(1)求椭圆方程;
(2)若 ![]() ,求直线PQ的方程;
,求直线PQ的方程;
(3)M,N为椭圆上关于x轴对称的两点,直线PM,PN分别与x轴交于R,S,求证:|OR||OS|为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com