
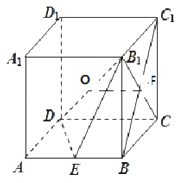
【题目】如图,在正方体ABCD﹣A1B1C1D1的棱长为a,若E为棱AB的中点,
①求四棱锥B1﹣BCDE的体积
②求证:面B1DC⊥面B1DE.

【答案】①![]() ;②见解析.
;②见解析.
【解析】试题分析:
①由正方体的性质可得B1B⊥平面BEDC,结合棱锥的体积公式计算可得四棱锥B1﹣BCDE的体积V=![]() ;
;
②取B1D的中点O,设BC1∩B1C=F,连接OF,由题意可得四边形OEBF是平行四边形,结合正方体的性质可得OE⊥DC,OE⊥B1C,故OE⊥平面B1DC,结合面面垂直的判断定理可得平面B1DC⊥面B1DE.
试题解析:
①由正方体的性质可得B1B⊥平面BEDC,
∴四棱锥B1﹣BCDE的体积V=![]() S梯形BCDEB1B=
S梯形BCDEB1B=![]()
![]() (a+
(a+![]() a)aa=
a)aa=![]() ;
;
②取B1D的中点O,设BC1∩B1C=F,连接OF,
∵O,F分别是B1D与B1C的中点,∴OF∥DC,且OF=![]() DC,
DC,
又∵E为AB中点,∴EB∥DC,且EB=![]() DC,
DC,
∴OF∥EB,OF=EB,即四边形OEBF是平行四边形,∴OE∥BF,
∵DC⊥平面BCC1B1 , BC1平面BCC1B1 , ∴BC1⊥DC,∴OE⊥DC.
又BC1⊥B1C,∴OE⊥B1C,又∵DC平面B1DC,B1C平面B1DC,DC∩B1C=C,
∴OE⊥平面B1DC,又∵OE平面B1DE,∴平面B1DC⊥面B1DE.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人都准备于下午12:00-13:00之间到某车站乘某路公交车外出,设在12:00-13:00之间有四班该路公交车开出,已知开车时间分别为12:20,12:30,12:40,13:00,分别求他们在下述情况下坐同一班车的概率.
(1)他们各自选择乘坐每一班车是等可能的;
(2)他们各自到达车站的时刻是等可能的(有车就乘).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点,x轴的正半轴为极轴的极坐标系中,曲线C1的极坐标方程为ρ=2sinθ,正方形ABCD的顶点都在C1上,且依次按逆时针方向排列,点A的极坐标为( ![]() ,
, ![]() ).
).
(1)求点C的直角坐标;
(2)若点P在曲线C2:x2+y2=4上运动,求|PB|2+|PC|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的可导函数f(x),其导函数记为f'(x),满足f(x)+f(2﹣x)=(x﹣1)2 , 且当x≤1时,恒有f'(x)+2<x.若 ![]() ,则实数m的取值范围是( )
,则实数m的取值范围是( )
A.(﹣∞,1]
B.![]()
C.[1,+∞)
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知M是正四面体ABCD棱AB的中点,N是棱CD上异于端点C,D的任一点,则下列结论中,正确的个数有( )
(1)MN⊥AB;
(2)若N为中点,则MN与AD所成角为60°;
(3)平面CDM⊥平面ABN;
(4)不存在点N,使得过MN的平面与AC垂直.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直四棱柱ABCD﹣A1B1C1D1内接于半径为 ![]() 的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( )
的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( ) 
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱锥P﹣ABCD中,底面ABCD的边长为4,PD=4,E为PA的中点, 
(1)求证:平面EBD⊥平面PAC;
(2)求直线BE与平面PBD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲罐中有![]() 个红球,
个红球,![]() 个白球和
个白球和![]() 个黑球,乙罐中有
个黑球,乙罐中有![]() 个红球,
个红球,![]() 个白球和
个白球和![]() 个黑球。先从甲罐中随机取出一球放入乙罐,分别以
个黑球。先从甲罐中随机取出一球放入乙罐,分别以![]() 和
和![]() 表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以
表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以![]() 表示由乙罐取出的球是红球的事件,则下列结论中正确的是________(写出所有正确结论的编号)。
表示由乙罐取出的球是红球的事件,则下列结论中正确的是________(写出所有正确结论的编号)。
①![]() ; ② 事件
; ② 事件![]() 与事件
与事件![]() 相互独立;③
相互独立;③![]()
④![]() 是两两互斥的事件;
是两两互斥的事件;
⑤![]() 的值不能确定,因为它与
的值不能确定,因为它与![]() 中哪一个发生有关
中哪一个发生有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() (图1)的三视图如图2所示,
(图1)的三视图如图2所示,![]() 为正三角形,
为正三角形,![]() 垂直底面
垂直底面![]() ,俯视图是直角梯形.
,俯视图是直角梯形.


图1 图2
(1)求正视图的面积;
(2)求四棱锥![]() 的体积;
的体积;
(3)求证:![]() 平面
平面![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com