
分析 由已知结合数列递推式求出数列前几项,猜测、归纳出数列的通项公式,然后利用数学归纳法证明.
解答 解:由an+1=$\frac{n}{n+1}$an+1,且a1=1得:
${a}_{2}=\frac{1}{2}×1+1=\frac{3}{2}$,${a}_{3}=\frac{2}{3}{a}_{2}+1=\frac{2}{3}×\frac{3}{2}+1=2=\frac{4}{2}$,
${a}_{4}=\frac{3}{4}{a}_{3}+1=\frac{3}{4}×2+1=\frac{5}{2}$,${a}_{5}=\frac{4}{5}{a}_{4}+1=\frac{4}{5}×\frac{5}{2}+1=\frac{6}{2}$,
…
由此猜测:${a}_{n}=\frac{n+1}{2}$.
下面利用数学归纳法证明:
${a}_{1}=1=\frac{2}{2}=\frac{1+1}{2}$,命题成立;
假设n=k(k∈N*且k≥1)命题成立,即${a}_{k}=\frac{k+1}{2}$,
则当n=k+1时,${a}_{k+1}=\frac{k}{k+1}{a}_{k}+1=\frac{k}{k+1}•\frac{k+1}{2}+1=\frac{k+2}{2}$=$\frac{(k+1)+1}{2}$,命题成立.
综上,对于任意n∈N*,都有${a}_{n}=\frac{n+1}{2}$成立.
故答案为:$\frac{n+1}{2}$.
点评 本题考查数列递推式,考查了利用猜测、归纳的方法求数列的通项公式,训练了利用数学归纳法证明与自然数有关的命题的方法,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 180 | C. | 6$\sqrt{3}$ | D. | 6$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
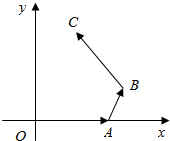 如图,在平面直角坐标系中,$|\overrightarrow{OA}|=2|\overrightarrow{AB}|=2$,∠OAB=$\frac{2π}{3}$,$\overrightarrow{BC}=(-1,\sqrt{3})$,求点B,C的坐标.
如图,在平面直角坐标系中,$|\overrightarrow{OA}|=2|\overrightarrow{AB}|=2$,∠OAB=$\frac{2π}{3}$,$\overrightarrow{BC}=(-1,\sqrt{3})$,求点B,C的坐标.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {an•an+1} | B. | {nan} | C. | {${a}_{n}^{2}$} | D. | $\frac{{a}_{n}}{{a}_{n+1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com