
【题目】已知点F(1,0),直线l:x=﹣1,直线l'垂直l于点P,线段PF的垂直平分线交l'于点Q.
(1)求点Q的轨迹方程C;
(2)过F做斜率为 ![]() 的直线交C于A,B,过B作l平行线交C于D,求△ABD外接圆的方程.
的直线交C于A,B,过B作l平行线交C于D,求△ABD外接圆的方程.
【答案】
(1)解:由垂直平分线的性质可知:PQ=PF,结合抛物线的定义可得Q点的轨迹方程是以F点为焦点,以直线l为准线的抛物线,其轨迹方程C为:y2=4x.
(2)由题意可得,直线l的方程为: ![]() ,
,
与抛物线方程C联立整理可得:y2﹣8y﹣4=0,则:y1+y2=8,y1y2=﹣4,
很明显△ABD外接圆的圆心为线段AB的垂直平分线与x轴的交点,
设AB中点为E,则 ![]() ,
,
中垂线方程为:y﹣4=﹣2(x﹣9),令y=0可得圆心坐标为:(11,0),
利用弦长公式: ![]() ,
,
圆心到直线AB:x﹣2y﹣1=0的距离为: ![]() ,
,
设圆的半径为R,据此有: ![]() ,
,
则△ABD外接圆的方程是(x﹣11)2+y2=120.
【解析】(1)由垂直平分线的性质可知:PQ=PF,结合抛物线的定义可得Q点的轨迹方程是以F点为焦点,以直线l为准线的抛物线,其轨迹方程C为:y2=4x.(2)根据题意设直线方程为:y = ![]() ( x 1 ),联立抛物线方程,根据韦达定理得到y1+y2, y1y2, 很明显△ABD外接圆的圆心为线段AB的垂直平分线与x轴的交点,可得到中点E的坐标,进而得到中垂线方程,当y=0时,得到圆心坐标,根据勾股定理可解得R,从而的到外接圆的方程.
( x 1 ),联立抛物线方程,根据韦达定理得到y1+y2, y1y2, 很明显△ABD外接圆的圆心为线段AB的垂直平分线与x轴的交点,可得到中点E的坐标,进而得到中垂线方程,当y=0时,得到圆心坐标,根据勾股定理可解得R,从而的到外接圆的方程.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为矩形,M是AD上一点.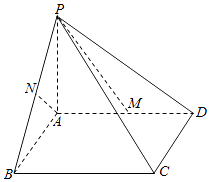
(1)求证:AB⊥PM;
(2)若N是PB的中点,且AN∥平面PCM,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,右焦点为F,右顶点为E,P为直线x=
,右焦点为F,右顶点为E,P为直线x= ![]() a上的任意一点,且(
a上的任意一点,且( ![]() +
+ ![]() )
) ![]() =2.
=2.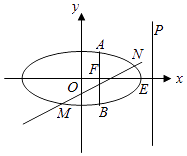
(Ⅰ)求椭圆C的方程;
(Ⅱ)过F垂直于x轴的直线AB与椭圆交于A,B两点(点A在第一象限),动直线l与椭圆C交于M,N两点,且M,N位于直线AB的两侧,若始终保持∠MAB=∠NAB,求证:直线MN的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f(x)=anxn+an﹣1xn﹣1+…+a1x+a0的值的秦九韶算法,即将f(x)改写成如下形式:f(x)=(…((anx+an﹣1)x+an﹣2)x+…+a1)x+a0 , 首先计算最内层一次多项式的值,然后由内向外逐层计算一次多项式的值,这种算法至今仍是比较先进的算法,将秦九韶算法用程序框图表示如图,则在空白的执行框内应填入( )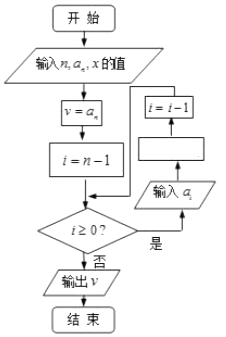
A.v=vx+ai
B.v=v(x+ai)
C.v=aix+v
D.v=ai(x+v)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)证明:k∈R,直线y=g(x)都不是曲线y=f(x)的切线;
(2)若x∈[e,e2],使得f(x)≤g(x)+ ![]() 成立,求实数k的取值范围.
成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}是公差为d(d≠0)的等差数列,Sn为其前n项和,a1 , a2 , a5成等比数列.
(Ⅰ)证明S1 , S3 , S9成等比数列;
(Ⅱ)设a1=1,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,△ABC是正三角形,△ACP是直角三角形,∠ABP=∠CBP,AB=BP.
(1)证明:平面ACP⊥平面ABC;
(2)若E为棱PB与P不重合的点,且AE⊥CE,求AE与平面ABC所成的角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com