Question

【题目】如图，在四棱锥中，底面是直角梯形，侧棱底面， 垂直于和，为棱上的点，，.

（1）若为棱的中点，求证：//平面；

（2）当时，求平面与平面所成的锐二面角的余弦值；

（3）在第（2）问条件下，设点是线段上的动点，与平面所成的角为，求当取最大值时点的位置.

Answer 1

【答案】（1）见解析；（2）；（3）即点N在线段CD上且

【解析】

（1）取线段SC的中点E，连接ME，ED．可证是平行四边形，从而有，则可得线面平行；

（2）以点A为坐标原点，建立分别以AD、AB、AS所在的直线为x轴、y轴、z轴建立空间直角坐标系，求出两平面与平面的法向量，由法向量夹角的余弦值可得二面角的余弦值；

（3）设，其中，求出，由MN与平面所成角的正弦值为与平面的法向量夹角余弦值的绝对值可求得结论．

（1）证明：取线段SC的中点E，连接ME，ED．

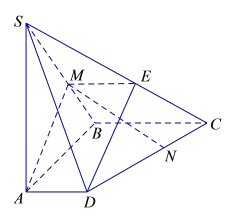
在中，ME为中位线，∴且，

∵且，∴且，

∴四边形AMED为平行四边形．

∴．

∵平面SCD，平面SCD，

∴平面SCD．

（2）解：如图所示以点A为坐标原点，建立分别以AD、AB、AS所在的直线为x轴、y轴、z轴建立空间直角坐标系，则，，，，，

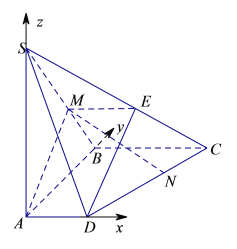
由条件得M为线段SB近B点的三等分点．

于是，即，

设平面AMC的一个法向量为，则，

将坐标代入并取，得．

另外易知平面SAB的一个法向量为，

所以平面AMC与平面SAB所成的锐二面角的余弦为．

（3）设，其中．

由于，所以．

所以，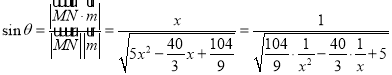

可知当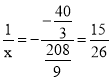，即时分母有最小值，此时有最大值，

此时，，即点N在线段CD上且．