
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)令![]() ,讨论函数
,讨论函数![]() 的零点的个数;
的零点的个数;
(3)若![]() ,正实数
,正实数![]() 满足
满足![]() ,证明:
,证明: ![]() .
.
【答案】(1)2x﹣y﹣1=0;(2)见解析;(3)见解析.
【解析】试题分析:(1)求出函数的导数,计算![]() ,求出切线方程即可;
,求出切线方程即可;
(Ⅱ)求出函数的导数,通过讨论![]() 的范围,根据函数的单调区间和函数的极值即可讨论函数
的范围,根据函数的单调区间和函数的极值即可讨论函数![]() 的零点的个数;;
的零点的个数;;
(Ⅲ)得到![]() 令
令![]() ,则
,则![]() ,根据函数的单调性求出
,根据函数的单调性求出![]() ,证明结论即可.
,证明结论即可.
试题解析:
(1)当a=0时,f(x)= lnx+x,
则f(1)=1,所以切点为(1,1),
又f′(x)= ![]() +1,则切线斜率k = f′(1)=2,
+1,则切线斜率k = f′(1)=2,
故切线方程为:y﹣1=2(x﹣1),即2x﹣y﹣1=0
(2)g(x)=f(x)﹣(ax﹣1)=lnx﹣![]() ax2+(1﹣a)x+1,
ax2+(1﹣a)x+1,
所以g′(x)=![]() ﹣ax+(1﹣a)=
﹣ax+(1﹣a)=![]() ,
,
当a≤0时,因为x>0,所以g′(x)>0.
所以g(x)在(0,+∞)上是递增函数
而![]()
所以函数![]() 有且只有一个零点
有且只有一个零点
当0<a<1时,g′(x)=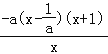 ,
,
令g′(x)=0,得x=![]() ,
,
所以当x∈(0,![]() )时,g′(x)>0;当x∈(
)时,g′(x)>0;当x∈(![]() ,+∞)时,g′(x)<0,
,+∞)时,g′(x)<0,
因此函数g(x)在x∈(0,![]() )是增函数,在(
)是增函数,在(![]() ,+∞)是减函数,
,+∞)是减函数,
∴x=![]() 时,g(x)有极大值g(
时,g(x)有极大值g(![]() )=
)=![]() ﹣lna>0
﹣lna>0
又![]()
∴当0<a<1时函数![]() 有两个零点
有两个零点
(3)证明:当![]()
所以![]()
即为: ![]()
所以![]()
令![]()
![]()
所以![]()
所以![]()
所以![]()
因为![]()


科目:高中数学 来源: 题型:
【题目】给出下列命题:①已知 ![]() ,“
,“ ![]() 且
且 ![]() ”是“
”是“ ![]() ”的充分条件;
”的充分条件;
②已知平面向量 ![]() ,
, ![]() 是“
是“ ![]() ”的必要不充分条件;
”的必要不充分条件;
③已知 ![]() ,“
,“ ![]() ”是“
”是“ ![]() ”的充分不必要条件;
”的充分不必要条件;
④命题 ![]() “
“ ![]() ,使
,使 ![]() 且
且 ![]() ”的否定为
”的否定为 ![]() “
“ ![]() ,都有
,都有 ![]() 且
且 ![]() ”.其中正确命题的个数是( )
”.其中正确命题的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在圆
在圆![]() :
: ![]() 上,而
上,而![]() 为
为![]() 在
在![]() 轴上的投影,且点
轴上的投影,且点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 是曲线
是曲线![]() 上两点,且
上两点,且![]() ,
, ![]() 为坐标原点,求
为坐标原点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018福建福州市一中高三上学期期中考试】已知椭圆![]() :
: ![]() 的右焦点为
的右焦点为![]() ,点
,点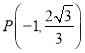 在椭圆上,且
在椭圆上,且![]() 与
与![]() 轴交点恰为
轴交点恰为![]() 中点.
中点.
(I)求椭圆![]() 的方程;
的方程;
(II)过![]() 作两条互相垂直的直线,分别交椭圆
作两条互相垂直的直线,分别交椭圆![]() 于点
于点![]() 和
和![]() .求四边形
.求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省![]() 情况图,则下列陈述正确的是( )
情况图,则下列陈述正确的是( )
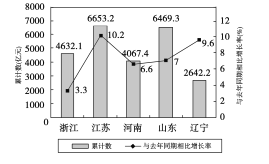
①2017年第一季度 ![]() 总量和增速均居同一位的省只有1个;
总量和增速均居同一位的省只有1个;
②与去年同期相比,2017年第一季度五个省的![]() 总量均实现了增长;
总量均实现了增长;
③去年同期的![]() 总量前三位是江苏、山东、浙江;
总量前三位是江苏、山东、浙江;
④2016年同期浙江的![]() 总量也是第三位.
总量也是第三位.
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的一条对称轴为
的一条对称轴为![]() ,且最高点的纵坐标是
,且最高点的纵坐标是![]() .
.
(1)求![]() 的最小值及此时函数
的最小值及此时函数![]() 的最小正周期、初相;
的最小正周期、初相;
(2)在(1)的情况下,设![]() ,求函数
,求函数![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com