
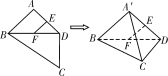
【题目】如图,平面四边形ABCD中,E,F是AD,BD中点,![]() ,
,![]() ,将
,将![]() 沿对角线BD折起至
沿对角线BD折起至![]() ,使平面
,使平面![]() 平面BCD,则四面体
平面BCD,则四面体![]() 中,下列结论不正确的是( )
中,下列结论不正确的是( )
A.![]() 平面
平面![]()
B.异面直线CD与![]() 所成的角为
所成的角为![]()
C.异面直线EF与![]() 所成的角为
所成的角为![]()
D.直线![]() 与平面BCD所成的角为
与平面BCD所成的角为![]()
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,动点
中,动点![]() 与两定点
与两定点![]() ,
,![]() 连线的斜率之积为
连线的斜率之积为![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() ,过原点
,过原点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点(点
两点(点![]() 在第一象限),求四边形
在第一象限),求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家文明城市评审委员会对甲、乙两个城市是否能入围“国家文明城市”进行走访调查,派出10人的调查组,先后到甲、乙两个城市的街道、社区进行问卷调查,然后打分(满分100分),他们给出甲、乙两个城市分数的茎叶图如图所示:
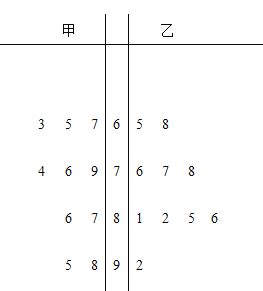
(1)请你用统计学的知识分析哪个城市更应该入围“国家文明城市”,并说明理由;
(2)从甲、乙两个城市的打分中各抽取2个,在已知有大于80分的条件下,求抽到乙城市的分数都小于80分的概率.
(参考数据:![]() ,
,![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是
是![]() 且边长为
且边长为![]() 的菱形,侧面
的菱形,侧面![]() 为正三角形,其所在平面垂直于底面
为正三角形,其所在平面垂直于底面![]() .
.

(1)若![]() 为
为![]() 边的中点,求证:
边的中点,求证:![]() 平面
平面![]() .
.
(2)求证:![]() .
.
(3)若![]() 为
为![]() 边的中点,能否在
边的中点,能否在![]() 上找出一点
上找出一点![]() ,使平面
,使平面 ![]() 平面
平面![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个命题:①在匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;②若两个变量的线性相关性越强,则相关系数的绝对值越接近于1;③对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,判断“
越小,判断“![]() 与
与![]() 有关系”的把握越大;其中真命题的个数为( )
有关系”的把握越大;其中真命题的个数为( )
A.3B.2C.1D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,国家深入推进精准脱贫,加大资金投入,强化社会帮扶,为了更好的服务于人民,派调查组到某农村去考察和指导工作.该地区有100户农民,且都从事水果种植,据了解,平均每户的年收入为2万元.为了调整产业结构,调查组和当地政府决定动员部分农民从事水果加工,据估计,若能动员![]() 户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高
户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高![]() ,而从事水果加工的农民平均每户收入将为
,而从事水果加工的农民平均每户收入将为![]() 万元.
万元.
(1)若动员![]() 户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求
户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这100户农民中从事水果加工的农民的总收入始终不高于从事水果种植的农民的总收入,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() 当
当![]() 时,判断直线
时,判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
![]() 若直线
若直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的四个顶点恰好是一边长为2,一内角为
的四个顶点恰好是一边长为2,一内角为![]() 的菱形的四个顶点.
的菱形的四个顶点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,在直线
两点,在直线![]() 上存在点
上存在点![]() ,使得
,使得![]() 为等边三角形,求
为等边三角形,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com