
x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.求:
(Ⅰ)输出的x(x<6)的概率;
(Ⅱ)输出的x(6<x≤8)的概率.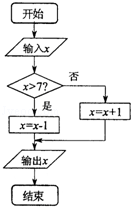
(Ⅰ) ;(Ⅱ)
;(Ⅱ)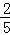 .
.
解析试题分析:(Ⅰ)由已知中的程序框图,我们根据选择结构的功能,可分析出程序的功能是计算并输出分段函数y=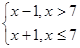 的函数值,输出的x(x<6),可得x<5,即可求出输出的x(x<6)的概率;
的函数值,输出的x(x<6),可得x<5,即可求出输出的x(x<6)的概率;
(Ⅱ)由输出的结果在区间6<x 8上,我们可以分当x
8上,我们可以分当x 7时和x>7时两种情况,分别讨论满足条件的x的取值范围,得到输出结果的范围,最后根据输入x的取值范围利用几何概型求出概率即可.
7时和x>7时两种情况,分别讨论满足条件的x的取值范围,得到输出结果的范围,最后根据输入x的取值范围利用几何概型求出概率即可.
试题解析:
(Ⅰ)由已知中的程序框图可得
该程序的功能是计算并输出分段函数y=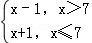 的函数值,
的函数值,
当x<6时,输出x+1,此时输出的结果满足x+1<6,所以x<5,
所以输出的x(x<6)的概率为P=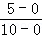 =
= ;
;
(Ⅱ)当x≤7时,输出x+1,此时输出的结果满足6<x+1≤8
解得5<x≤7;
当x>7时,输出x﹣1,此时输出的结果满足6<x﹣1≤8
解得7<x≤9;
综上,输出的x的范围中5<x≤9.
则使得输出的x满足6<x≤8的概率为P=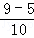 =
=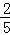 .
.
考点:1.程序框图;2.几何概率.


科目:高中数学 来源: 题型:解答题
形状如图所示的三个游戏盘中(图(1)是正方形,M、N分别是所在边中点,图(2)是半径分别为2和4的两个同心圆,O为圆心,图(3)是正六边形,点P为其中心)各有一个玻璃小球,依次水平摇动三个游戏盘,当小球静止后,就完成了一局游戏.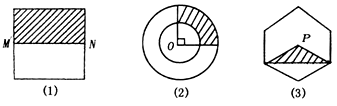
(Ⅰ)一局游戏后,这三个盘中的小球都停在阴影部分的概率是多少?
(Ⅱ)用随机变量ξ表示一局游戏后,小球停在阴影部分的事件个数与小球没有停在阴影部分的事件个数之差的绝对值,求随机变量ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
春节期间,某商场决定从3种服装、2种家电、3种日用品中,选出3种商品进行促销活动。
⑴)试求选出的3种商品中至少有一种是家电的概率;
⑵商场对选出的某商品采用抽奖方式进行促销,即在该商品现价的基础上将价格提高100元,规定购买该商品的顾客有3次抽奖的机会:若中一次奖,则获得数额为 元的奖金;若中两次奖,则共获得数额为
元的奖金;若中两次奖,则共获得数额为 元的奖金;若中3次奖,则共获得数额为
元的奖金;若中3次奖,则共获得数额为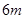 元的奖金。假设顾客每次抽奖中获的概率都是
元的奖金。假设顾客每次抽奖中获的概率都是 ,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?
,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设有关于 的一元二次方程
的一元二次方程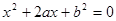
(1)若 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数,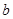 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若 是从区间[0,3]任取的一个数,
是从区间[0,3]任取的一个数,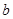 是从区间[0,2]任取的一个数,求上述方程有实根的概率.
是从区间[0,2]任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(1)求张同学至少取到1道乙类题的概率;
(2)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对每道甲类题的概率都是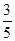 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是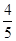 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用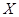 表示张同学答对题的个数,求
表示张同学答对题的个数,求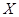 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
甲乙两艘轮船都要停靠同一个泊位,它们可以在一昼夜(零点至24点)的任意时刻到达,设甲、乙两艘轮船停靠泊位的时间分别是3小时和5小时,则有一艘轮船停靠泊位时必须等待一段时间的概率为____(用分数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com