
【题目】设f(x)=a(x-5)2+6lnx,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图, ![]() 表示神风摩托车厂一天的销售收入与摩托车销售量的关系;
表示神风摩托车厂一天的销售收入与摩托车销售量的关系; ![]() 表示摩托车厂一天的销售成本与销售量的关系.
表示摩托车厂一天的销售成本与销售量的关系.
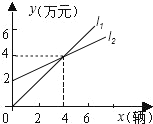
(1)写出销售收入与销售量之间的函数关系式;
(2)写出销售成本与销售量之间的函数关系式;
(3)当一天的销售量为多少辆时,销售收入等于销售成本;
(4)当一天的销售超过多少辆时,工厂才能获利?(利润=收入-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x),f(0)=-2,且对![]() ,y
,y![]() R,都有f(x+y)-f(y)=(x+2y+1)x.
R,都有f(x+y)-f(y)=(x+2y+1)x.
(1)求f(x)的表达式;
(2)已知关于x的不等式f(x)-ax+a+1![]() 的解集为A,若A[2,3],求实数a的取值范围;
的解集为A,若A[2,3],求实数a的取值范围;
(3)已知数列{![]() }中,
}中, ![]() ,
, ![]() ,记
,记![]() ,且数列{
,且数列{![]() 的前n项和为
的前n项和为![]() ,
,
求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙H被直线x-y-1=0,x+y-3=0分成面积相等的四个部分,且截x轴所得线段的长为2。
(I)求⊙H的方程;
(Ⅱ)若存在过点P(0,b)的直线与⊙H相交于M,N两点,且点M恰好是线段PN的中点,求实数b的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间。按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。

区间 |
|
|
|
|
|
人数 |
| a | b |
(1)求正整数a,b,N的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组中抽取的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1 人在第3组的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() ,点
,点![]() 是圆上一动点,
是圆上一动点, ![]() 的垂直平分线与
的垂直平分线与![]() 交于点
交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 且斜率不为0的直线
且斜率不为0的直线![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明直线
,证明直线![]() 过定点,并求
过定点,并求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com