练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知sinα+cosα=-$\sqrt{2}$，则tanα+$\frac{1}{tanα}$的值等于（　　）
    A．2B．$\frac{1}{2}$C．-2D．-$\frac{1}{2}$

    分析 由已知条件求出sinαcosα的值，利用切化弦化简所求表达式代入求解即可．

    解答 解：∵sinα+cosα=-$\sqrt{2}$，
    ∴（sinα+cosα）2=（-$\sqrt{2}$）2，
    解得sinαcosα=$\frac{1}{2}$，
    ∴tanα+$\frac{1}{tanα}$=$\frac{sinα}{cosα}$+$\frac{cosα}{sinα}$=$\frac{si{n}^{2}α+co{s}^{2}α}{sinαcosα}$=$\frac{1}{\frac{1}{2}}$=2．
    故选：A．

    点评 本题考查三角函数的化简求值，同角三角函数的基本关系式的应用，基本知识的考查．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．已知$f（x）=\frac{{{2^x}-1}}{{{2^x}+1}}$，
    （Ⅰ）判断f（x）的奇偶性；
    （Ⅱ）判断函数f（x）的单调性，并用单调性定义证明之；
    （Ⅲ）求f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知x，y的取值如表所示，
    x01234 
    y2.33.94.65.1 6.6
    从所得散点图分析，y与x线性相关，且$\widehat{y}$=0.98x+a，则a的值为（　　）
    A．2.45B．2.54C．2.64D．3.04

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．设全集A={1，2，3，4，5}，B={2，4，6，8，10}，则A∪B=（　　）
    A．{2，4}B．{1，2，3，4，5，6，8，10}
    C．{1，2，3，4，5}D．{2，4，6，8，10}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{4}$=1的一条渐近线方程为y=2x，其实轴长为（　　）
    A．1B．2C．4D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

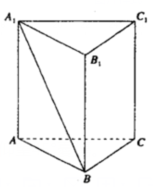    10．如图，在三棱柱ABC-A1B1C1中，底面ABC为正三角形，侧棱AA1⊥面ABC，若AB=AA1，则直线A1B与AC所成角的余弦值为（　　）
    A．$\frac{\sqrt{2}}{2}$B．$\frac{\sqrt{2}}{4}$C．$\frac{\sqrt{14}}{2}$D．$\frac{\sqrt{14}}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．i是虚数单位，复数$\frac{4i}{1-i}$等于（　　）
    A．-2-2iB．2-2iC．-2+2iD．2+2i

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．若向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-3，4），则$\overrightarrow{a}$•$\overrightarrow{b}$的值等于5；$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦值等于$\frac{\sqrt{5}}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

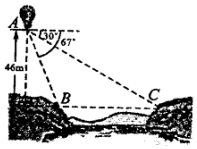    15．如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为67°，30°，此时气球的高是46m，则河流的宽度BC约等于60m．（用四舍五入法将结果精确到个位．参考数据：sin67°≈0.92，cos67°≈0.39，sin37°≈0.60，cos37°≈0.80，$\sqrt{3}$≈1.73．

    查看答案和解析>>

    同步练习册答案