
【题目】已知四棱锥P﹣ABCD的底面ABCD是平行四边形,△PAB与△ABC是等腰三角形,PA⊥平面ABCD,PA=2,AD=2 ![]() ,AC⊥BA,点E是线段AB上靠近点B的一个三等分点,点F、G分别在线段PD,PC上.
,AC⊥BA,点E是线段AB上靠近点B的一个三等分点,点F、G分别在线段PD,PC上. 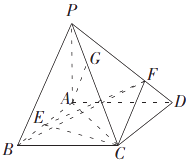
(Ⅰ)证明:CD⊥AG;
(Ⅱ)若三棱锥E﹣BCF的体积为 ![]() ,求
,求 ![]() 的值.
的值.
【答案】解:(Ⅰ)证明:依题意,因为AB∥CD,AC⊥BA,所以AC⊥CD. 又因为PA⊥底面ABCD,所以PA⊥CD,
因为AC∩PA=A,所以CD⊥平面PAC,
因为AG平面PAC,所以CD⊥AG.
(Ⅱ)解:设点F到平面ABCD的距离为d,
则 ![]() ,
,
由 ![]() ,得
,得 ![]() ,
,
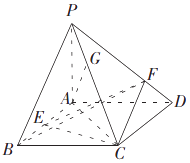
故 ![]() .
.
【解析】(Ⅰ)由AB∥CD,AC⊥BA,可得AC⊥CD.由PA⊥底面ABCD,可得PA⊥CD,可得CD⊥平面PAC,即可证明CD⊥AG.(II)设点F到平面ABCD的距离为d,利用三棱锥的体积计算公式可得:VE﹣BCF=VF﹣BEC , 可得d,进而得出答案.
【考点精析】本题主要考查了空间中直线与直线之间的位置关系的相关知识点,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某店销售进价为2元/件的产品![]() ,该店产品
,该店产品![]() 每日的销售量
每日的销售量![]() (单位:千件)与销售价格
(单位:千件)与销售价格![]() (单位:元/件)满足关系式
(单位:元/件)满足关系式![]() ,其中
,其中![]() .
.
(1)若产品![]() 销售价格为4元/件,求该店每日销售产品
销售价格为4元/件,求该店每日销售产品![]() 所获得的利润;
所获得的利润;
(2)试确定产品![]() 的销售价格,使该店每日销售产品
的销售价格,使该店每日销售产品![]() 所获得的利润最大.(保留1位小数)
所获得的利润最大.(保留1位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解甲、乙两名同学的数学学习情况,对他们的![]() 次数学测试成绩(满分
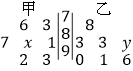
次数学测试成绩(满分![]() 分)进行统计,作出如下的茎叶图,其中
分)进行统计,作出如下的茎叶图,其中![]() 处的数字模糊不清,已知甲同学成绩的中位数是
处的数字模糊不清,已知甲同学成绩的中位数是![]() ,乙同学成绩的平均分是
,乙同学成绩的平均分是![]() 分.
分.
(1)求![]() 和
和![]() 的值;
的值;
(2)现从成绩在![]() 之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的概率.
之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,且过点M(4,1). (Ⅰ)求椭圆C的方程;
,且过点M(4,1). (Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l:y=x+m(m≠﹣3)与椭圆C交于P,Q两点,记直线MP,MQ的斜率分别为k1 , k2 , 试探究k1+k2是否为定值.若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代名著《九章算术》中有这样一段话:“今有金锤,长五尺,斩本一尺,重四斤.斩末一尺,重二斤.”意思是:“现有一根金锤,头部的1尺,重4斤;尾部的1尺,重2斤;且从头到尾,每一尺的重量构成等差数列.”则下列说法错误的是( )
A.该金锤中间一尺重3斤
B.中间三尺的重量和是头尾两尺重量和的3倍
C.该金锤的重量为15斤
D.该金锤相邻两尺的重量之差的绝对值为0.5斤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C1:ρsin2θ=4cosθ.以极点为坐标原点,极轴为x轴正半轴建立直角坐标系xOy,曲线C2的参数方程为: ![]() ,(θ∈[﹣
,(θ∈[﹣ ![]() ,
, ![]() ]),曲线C:
]),曲线C: 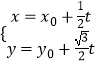 (t为参数).
(t为参数).
(Ⅰ)求C1的直角坐标方程;
(Ⅱ)C与C1相交于A,B,与C2相切于点Q,求|AQ|﹣|BQ|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,直线PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=4BE=4.
(I)求证:直线DE⊥平面PAC.
(Ⅱ)若直线PE与平面PAC所成的角的正弦值为 ![]() ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值.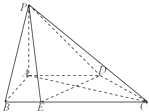
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com