[题目]已知数列{an}满足[2﹣(﹣1)n]an+[2+(﹣1)n]an+1=1+(﹣1)n×3n.则a25﹣a1= ．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知数列{an}满足[2﹣（﹣1）n]an+[2+（﹣1）n]an+1=1+（﹣1）n×3n，则a25﹣a1= ．

【答案】300
【解析】解：∵[2﹣（﹣1）n]an+[2+（﹣1）n]an+1=1+（﹣1）n×3n，

∴n=2k（k∈N*），可得：a2k+3a2k+1=1+6k，

n=2k﹣1（k∈N*），可得：3a2k﹣1+a2k=1﹣6k+3，

∴a2k+1﹣a2k﹣1=4k﹣1，

∴a25=（a25﹣a23）+（a23﹣a21）+…+（a3﹣a1）+a1

=（4×12﹣1）+（4×11﹣1）+…+（4×1﹣1）+a1= ﹣12+a1=300+a1．

则a25﹣a1=300，

所以答案是：300．

【考点精析】利用数列的通项公式对题目进行判断即可得到答案，需要熟知如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．

练习册系列答案

成长记寒假总动员云南科技出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】“大众创业，万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号．某生产企业积极响应号召，大力研发新产品，为了对新研发的一批产品进行合理定价，将该产品按事先拟定的价格进行试销，得到一组销售数据（xi ， yi）（i=1，2，…，6），如表所示：

试销单价x（元）	4	5	6	7	8	9
产品销量y（件）	q	84	83	80	75	68

已知 =80．
（Ⅰ）求出q的值；
（Ⅱ）已知变量x，y具有线性相关关系，求产品销量y（件）关于试销单价x（元）的线性回归方程；可供选择的数据：，
（Ⅲ）用表示用（Ⅱ）中所求的线性回归方程得到的与xi对应的产品销量的估计值．当销售数据（xi ， yi）对应的残差的绝对值时，则将销售数据（xi ， yi）称为一个“好数据”．现从6个销售数据中任取3个，求“好数据”个数ξ的分布列和数学期望E（ξ）．
（参考公式：线性回归方程中，的最小二乘估计分别为，）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某县一中计划把一块边长为20米的等边三角形ABC的边角地辟为植物新品种实验基地，图中DE需把基地分成面积相等的两部分，D在AB上，E在AC上．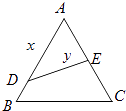
（1）设AD=x（x≥10），ED=y，试用x表示y的函数关系式；
（2）如果DE是灌溉输水管道的位置，为了节约，则希望它最短，DE的位置应该在哪里？如果DE是参观线路，则希望它最长，DE的位置又应该在哪里？说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

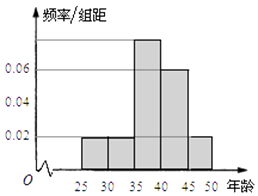
【题目】某单位280名员工参加“我爱阅读”活动，他们的年龄在25岁至50岁之间，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示．
（I）现要从年龄低于40岁的员工中用分层抽样的方法抽取12人，则年龄在第1，2，3组的员工人数分别是多少？
（II）为了交流读书心得，现从上述12人中再随机抽取3人发言，设3人中年龄在[35，40）的人数为ξ，求ξ的数学期望；
（III）为了估计该单位员工的阅读倾向，现对从该单位所有员工中按性别比例抽取的40人做“是否喜欢阅读国学类书籍”进行调查，调查结果如下表所示：（单位：人）