
【题目】如图,过抛物线y2=2px(p>0)焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( ) 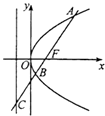
A.y2=3x
B.y2=9x
C.y2= ![]() x
x
D.y2= ![]() x
x
【答案】A
【解析】解:设A(x1 , y1),B(x2 , y2), 作AM、BN垂直准线于点M、N,则|BN|=|BF|,
又|BC|=2|BF|,得|BC|=2|BN|,
∴∠NCB=30°,
有|AC|=2|AM|=6,
设|BF|=x,则2x+x+3=6x=1,
而x1+ ![]() =3,x2+
=3,x2+ ![]() =1,且x1x2=
=1,且x1x2= ![]() ,
,
∴(3﹣ ![]() )(1﹣v)=
)(1﹣v)= ![]() ,解得p=
,解得p= ![]() .
.
得y2=3x.
故选A.
根据过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,作AM、BN垂直准线于点M、N,根据|BC|=2|BF|,且|AF|=3,和抛物线的定义,可得∠NCB=30°,设A(x1 , y1),B(x2 , y2),|BF|=x,而x1+ ![]() =3,x2+
=3,x2+ ![]() =1,且x1x2=
=1,且x1x2= ![]() ,即有(3﹣
,即有(3﹣ ![]() )(1﹣
)(1﹣ ![]() )=
)= ![]() ,可求得p的值,即求得抛物线的方程.
,可求得p的值,即求得抛物线的方程.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若直角坐标平面内的两点P、Q满足条件:
①P、Q都在函数y=f(x)的图象上;
②P、Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”(点对[P,Q]与[Q,P]看作同一对“友好点对”),
已知函数f(x)= ![]() ,则此函数的“友好点对”有( )
,则此函数的“友好点对”有( )
A.0对
B.1对
C.2对
D.3对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小组共10人,利用假期参加义工活动,已知参加义工活动次数为1,2,3的人数分别为2,4,4.现从这10人中随机选出2人作为该组代表参加座谈会.
(I)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率;
( II)设X为选出的2人参加义工活动次数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
(1)写出函数f(x)(x∈R)的解析式.
(2)若函数g(x)=f(x)+(4﹣2a)x+2(x∈[1,2]),求函数g(x)的最小值h(a).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年出现各种食品问题,食品添加剂会引起血脂增高、血压增高、血糖增高等疾病.为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
(1)请将如图的列联表补充完整;若用分层抽样的方法在患三高疾病的人群中抽![]() 人,其中女性抽多少人?
人,其中女性抽多少人?
(2)为了研究三高疾病是否与性别有关,请计算出统计量![]() ,并说明你有多大的把握认为三高疾病与性别有关?
,并说明你有多大的把握认为三高疾病与性别有关?
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|3≤3x≤27},B={x|log2x>1}. (Ⅰ)求A∩B,A∪B;
(Ⅱ)已知非空集合C={x|1<x≤a},若CA,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数g(x)=x2﹣2x+1+mlnx,(m∈R).
(1)当m=1时,求函数y=g(x)在点(1,0)处的切线方程;
(2)当m=﹣12时,求f(x)的极小值;
(3)若函数y=g(x)在x∈( ![]() ,+∞)上的两个不同的数a,b(a<b)处取得极值,记{x}表示大于x的最小整数,求{g(a)}﹣{g(b)}的值(ln2≈0.6931,ln3≈1.0986).
,+∞)上的两个不同的数a,b(a<b)处取得极值,记{x}表示大于x的最小整数,求{g(a)}﹣{g(b)}的值(ln2≈0.6931,ln3≈1.0986).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,分别是椭圆
,分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若点![]() 是第一象限内椭圆上的一点,
是第一象限内椭圆上的一点, ![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com