Question

【题目】等比数列{an}中，已知a1=1，a4=8，若a3 ， a5分别为等差数列{bn}的第4项和第16项．
（1）求数列{an}﹑{bn}的通项公式；
（2）令cn=anbn ， 求数列{cn}的前n项和Sn ．

Answer 1

【答案】
（1）解：设等比数列{an}公比为q，

∴a4=a1q3=8，即q3=8，即q=2，

∴an=a1qn﹣1=2n﹣1，

∴a3=4，a5=16，

∴b4=4，b16=16，

由等差数列公差为d，

∴d= = =1，

∴bn=b16+（n﹣16）×1=n，

数列{an}通项公式an=2n﹣1，{bn}的通项公式bn=n

（2）解：cn=anbn=n2n﹣1，

数列{cn}的前n项和Sn．

∴Sn=11+22+322+…+n2n﹣1，①

2Sn=12+222+323+…+n2n，②

①﹣②，得﹣Sn=1+2+22+…+2n﹣1﹣n2n，

= ﹣n2n，

=（1﹣n）2n﹣1，

Sn=（n﹣1）2n+1，

数列{cn}的前n项和Sn，Sn=（n﹣1）2n+1

【解析】（1）由等比数列的通项公式，代入即可求得公比q，由b4=4，b16=16，根据等差数列性质即可求得公差d，即可求得数列{an}﹑{bn}的通项公式；（2）由（1）可知：cn=anbn=n2n﹣1 ， 利用错位相减法能求出数列{cn}的前n项和Sn ．
【考点精析】认真审题，首先需要了解等比数列的通项公式（及其变式）(通项公式：)，还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系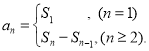)的相关知识才是答题的关键．